Задать булевую функцию в виде таблицы: На основе таблицы построить её СДНФ, найти номер функции

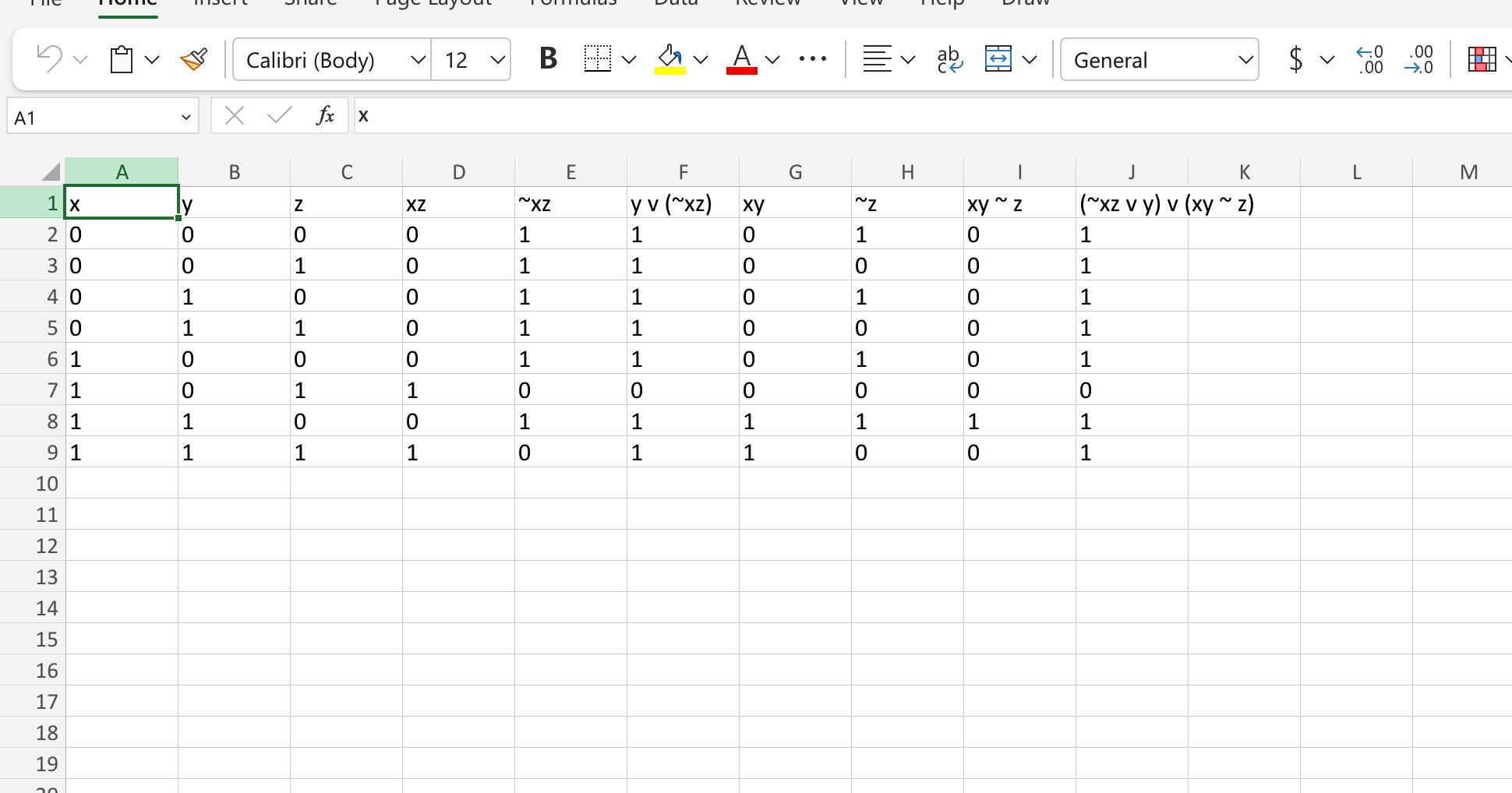
Ответ: Ваше логическое выражение xz -> y v (xy ~ z) x z → y v ( x y ~ z) эквивалентно (xz -> y) v (xy ~ z) ( x z → y) v ( x y ~ z), что можно упростить до (~xz v y) v (xy ~ z) ( ~ x z v y) v ( x y ~ z) с помощью законов импликации и де Моргана. Для построения таблицы истинности этой функции, нам нужно рассмотреть все возможные комбинации значений x, y и z x, y и z, которых всего восемь.

Для построения СДНФ (канонической дизъюнктивной нормальной формы) этой функции, нам нужно взять конъюнкцию переменных, соответствующих каждой строке таблицы, где значение функции равно 1, и объединить их дизъюнкцией. Таким образом, мы получим:

(~xz v y) v (xy ~ z) = (~x ~y ~z) v (~x ~y z) v (~x y ~z) v (~x y z) v (x ~y ~z) v (x y ~z) v (x y z)

Для нахождения номера функции, нам нужно записать значения функции в обратном порядке от последней строки таблицы к первой, и преобразовать полученную двоичную строку в десятичное число. Таким образом, мы получим:

(~xz v y) v (xy ~ z) = 11111011 в двоичной системе, что равно 251 в десятичной системе.