-
Спростіть вираз (x+1)(x-1)-(x+5)(x-5)+(x+1)(x-5) Розвʼяжіть рівняння (x-17)(x+17)=x²+6x-49
Ответы 2
-
Ответ:
Добре, почнемо зі спрощення виразу:
Спростимо вираз (x+1)(x-1)-(x+5)(x-5)+(x+1)(x-5):
(x+1)(x-1) = x^2 - 1
(x+5)(x-5) = x^2 - 25
(x+1)(x-5) = x^2 - 4x - 5
Отже, отримаємо:
x^2 - 1 - (x^2 - 25) + (x^2 - 4x - 5)
Після скорочення подібних членів:
x^2 - 1 - x^2 + 25 + x^2 - 4x - 5
Отримаємо:
-4x + 19
Тепер перейдемо до розв'язку рівняння:
(x-17)(x+17) = x^2 + 6x - 49
Розкладемо ліву частину:
x^2 + (17-17)x - 17*17 = x^2 + 6x - 49
x^2 - 289 = x^2 + 6x - 49
Відкинемо x^2 з обох сторін:
-289 = 6x - 49
Додамо 49 до обох сторін:
-240 = 6x
Розділимо обидві сторони на 6:
x = -40
Таким чином, після спрощення виразу ми отримали -4x + 19, а рішення рівняння x = -40.
-
Автор:
elian4vdd - 1 год назад
-
8
-
-
Решение на фото.....
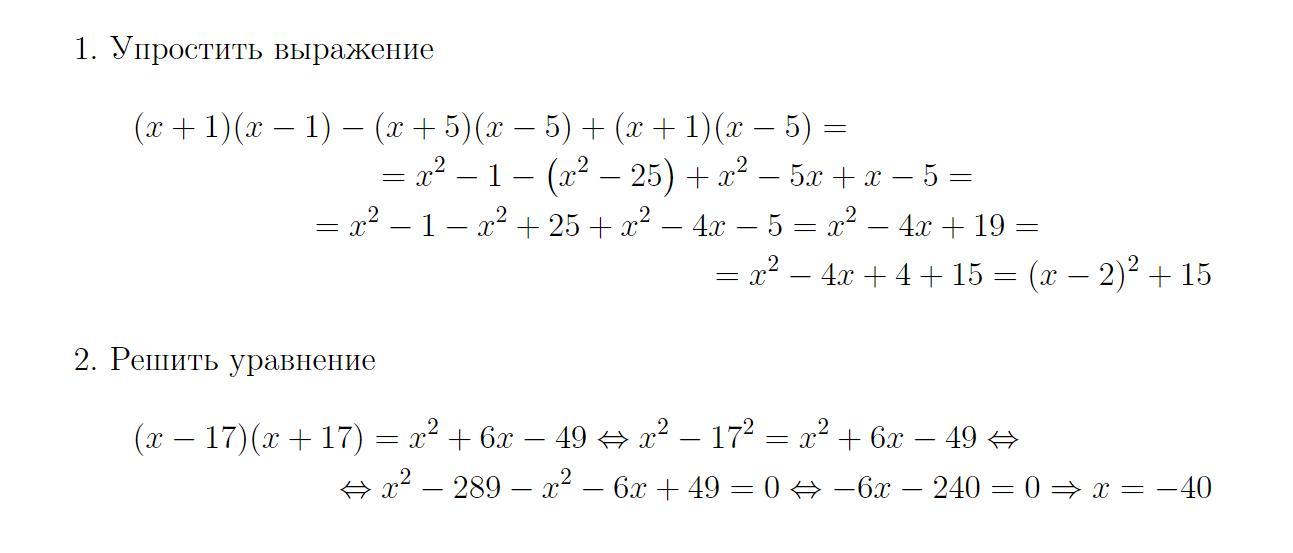
-
Автор:
marcelocaldwell - 1 год назад
-
10
-
-
Добавить свой ответ
-
100 БАЛЛОВЗаписать композицию С = В×А отношений А = {(3,3), (4,1), (4,2), (4,3), (4,4)} и В = {(1,1), (1,2), (1,3), (1,4), (2,2), (3,2), (3,4), (4,4) }. Проверить результаты за посредством операций над матрицами и графами заданных отношений
-
Предмет:
Математика -
Автор:
nolan58 - 1 год назад
-
Ответов:
1 -
Смотреть
-
-
Створити каліграми про природу
-
Предмет:
Українська література -
Автор:
fluffy16 - 1 год назад
-
Ответов:
1 -
Смотреть
-
-
Бросили две игральные кости. Событие А- сумма очков четна. Событие В – сумма очков меньше 8. Найти Р(А+В) и Р(А*В).
-
Предмет:
Математика -
Автор:
lizbethramsey - 1 год назад
-
Ответов:
2 -
Смотреть
-
- Охарактеризовать основных представителей алканов.
