-
Найдите: 3 3πa)cos2a u sin2a, если sina = 5' 2 < α <2πb) sin И COS 2 2' если cosa = √2 ,а е IV четвертиПожалуйста помогите нужен ответь срочно!!
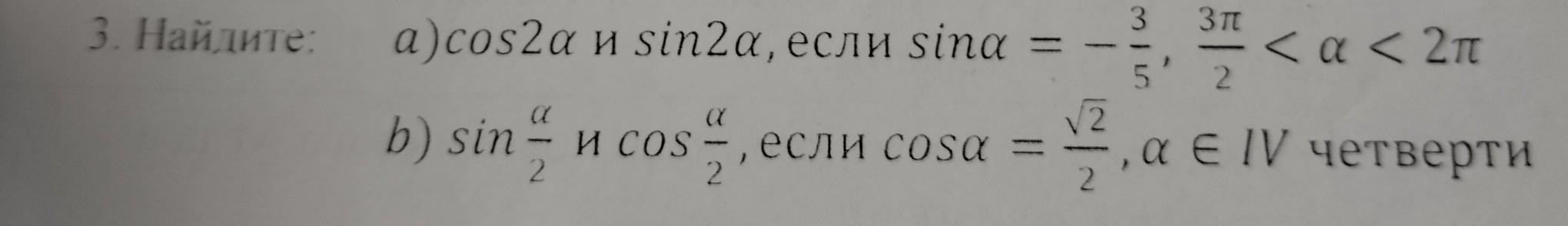
Ответы 1
-
Я попробую помочь вам решить эти задачи по тригонометрии.
Для начала, я исправлю некоторые ошибки в вашем вопросе:
- Вместо 3 3π вы, наверное, имели в виду 3π/3, то есть π.
- Вместо u вы, наверное, имели в виду и, то есть логическое умножение.
- Вместо 5' вы, наверное, имели в виду 5/2, то есть дробь.
Теперь я перепишу ваши задачи с учетом этих исправлений:
a) Найдите cos2α и sin2α, если sinα = 5/2 и 2π < α < 2π.
b) Найдите sin2β и cos2β, если cosβ = √2 и β в IV четверти.
Для решения этих задач, я буду использовать следующие формулы¹:
$$
\cos 2x = \cos^2 x - \sin^2 x
$$
$$
\sin 2x = 2 \sin x \cos x
$$
Также я буду пользоваться тригонометрической окружностью, чтобы определить знаки функций в разных четвертях.
Решение задачи a):
Если sinα = 5/2, то α лежит во II четверти, где sinα > 0 и cosα < 0.
Также, по теореме Пифагора, мы можем найти cosα:
$$
\cos^2 \alpha + \sin^2 \alpha = 1
$$
$$
\cos^2 \alpha + \left(\frac{5}{2}\right)^2 = 1
$$
$$
\cos^2 \alpha = 1 - \frac{25}{4} = -\frac{21}{4}
$$
$$
\cos \alpha = -\frac{\sqrt{21}}{2}
$$
Теперь мы можем найти cos2α и sin2α, используя формулы:
$$
\cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha = -\frac{21}{4} - \frac{25}{4} = -\frac{46}{4} = -\frac{23}{2}
$$
$$
\sin 2\alpha = 2 \sin \alpha \cos \alpha = 2 \cdot \frac{5}{2} \cdot -\frac{\sqrt{21}}{2} = -5\sqrt{21}
$$
Ответ: cos2α = -23/2, sin2α = -5√21.
Решение задачи b):
Если cosβ = √2, то β лежит в IV четверти, где cosβ > 0 и sinβ < 0.
Также, по теореме Пифагора, мы можем найти sinβ:
$$
\cos^2 \beta + \sin^2 \beta = 1
$$
$$
\left(\frac{\sqrt{2}}{2}\right)^2 + \sin^2 \beta = 1
$$
$$
\sin^2 \beta = 1 - \frac{1}{2} = \frac{1}{2}
$$
$$
\sin \beta = -\frac{\sqrt{2}}{2}
$$
Теперь мы можем найти sin2β и cos2β, используя формулы:
\sin 2\beta = 2 \sin \beta \cos \beta = 2 \cdot -\frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2}}{2} = -1
\cos 2\beta = \cos^2 \beta - \sin^2 \beta = \frac{1}{2} - \frac{1}{2} = 0
$$
Ответ: sin2β = -1, cos2β = 0.
Надеюсь, это было полезно для вас.
-
Автор:
conradthhn - 2 года назад
-
1
-
-
Добавить свой ответ
-
Задание 3. Определите, какой вид комического преобладает в рассказе «Аристократка». Воспользуйтесь приемом ПОПС-формула.
-
Предмет:
Литература -
Автор:
ignaciobentley - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Подберите десять глаголов с возвратным значением и запишите их во 2-м лице в единственном числе. ПОМОГИТЕ СРОЧНО!!!!
-
Предмет:
Русский язык -
Автор:
lamar - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
2. Выпиши предложение, в котором говорится, что Земля живая. большое начинается с маленького даю 20бл!
-
Предмет:
Литература -
Автор:
zayneraymond - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Русский контрольная работа
-
Предмет:
Русский язык -
Автор:
amyclark - 2 года назад
-
Ответов:
2 -
Смотреть
-
