-
Решите пожалуйста 2 системы...
[tex] \left \{ {{2 x^{2} -3xy+ y^{2} =0} \atop { y^{2}- x^{2}=12 }} ight. [/tex]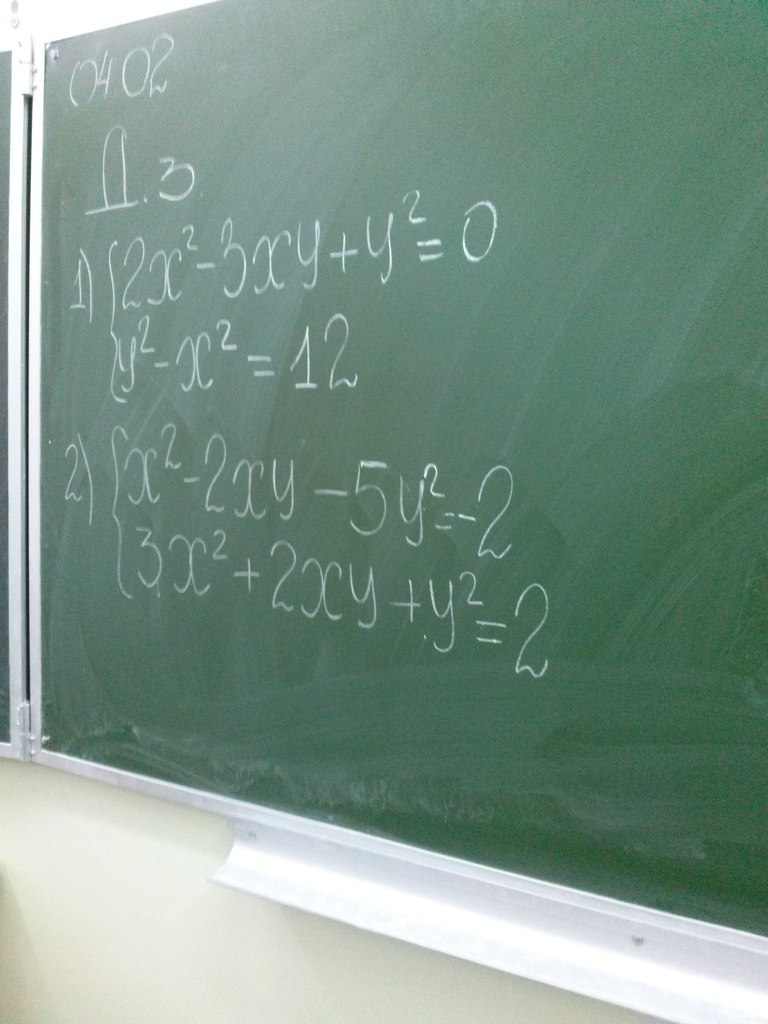
Ответы 2
-
1) решим первое уравнение как квадратное относительно х.2x^2 - 3y*x + y^2 = 0D=(-3y)^2 - 4*2*y^2 = y^2x1 = (3y + |y|)/4x2 = (3y - |y|)/4Подставляем каждое х во второе уравнение и ищем корни:y^2 - (9y^2 + 6y^2 + y^2)/16 = 1216y^2 - 16y^2 = 12*16 - не верно, значит х1 не является корнем.y^2 - (9y^2 - 6y^2 + y^2)/16 = 1216y^2 - 4y^2 = 12*1612y^2 = 12*16, y^2 = 16y = +-4 - значит х2 является корнем, найдем его:y = 4, x = (3*4 - 4)/4 = 2y = -4, x = (-12 - 4)/4 = -4Ответ: (2;4), (-4;-4)2) сложим оба уравнения, получим:4x^2 - 4y^2 = 0(x - y)(x + y) = 0x=y, x= -yx=y, y^2 - 2y^2 - 5y^2 = -2, -6y^2 = -2, y^2 = 1/3, y = +-√3/3x= -y, y^2 + 2y^2 - 5y^2 = -2, -2y^2 = -2, y^2 = 1, y = +-1Ответ: (-√3/3; -√3/3), (√3/3; √3/3); (-1;1), (1;-1)
-
Автор:
orionmorrow - 5 лет назад
-
0
-
-
1) из 1 ур-ия системы вычтем 2 и получим:
(*)из 2 ур-ия системы:
подставим в (*) вместо -12 выражение (x-y)(x+y)получим:3x(x-y)=(x-y)(x+y) и разделим на (x-y)≠03x=x+y2x=y подставим во 2 ур-ие системы и получим:
2) Сложим 1 и 2 ур-ия системы и получим:
Либо x=yлибо x=-yРассмотрим x=y.Подставим в 1 ур-ие системы:y²-2y²-5y²=-2-6y²=-2
Рассмотрим x=-y.Подставим в 1 ур-ие системы:y²+2y²-5y²=-2-2y²=-2y²=1
-
Автор:
zackfqm6 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Составить предложения на тему лето;три с восклицательным знаком и три с вопросительным.
-
Предмет:
Русский язык -
Автор:
matteobxio - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
арифметическая прогрессия
1) a1=-9
d=4
a43
2) -63; -58; -53.....
S14 ?
3)bn=3n-2
S120 -
Самая высокая гора на Кавказе?
-
Предмет:
География -
Автор:
princegg0s - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
помогите сделать звукобуквенный анализ.
Ежи,ежиха, ежата, ёжики.-
Предмет:
Русский язык -
Автор:
lucille68br - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
