-
На рисунке изображен график функции y=f(x). Пользуясь графиком, найдите:
1)f(-4), f(-2,5), f(0,5) f(2)
2)значения х, при которых f(x)=2,5; f(x)=1; f(x)=0;
3)область определения и область значения функции;
4)значения аргумента, при которых значения функции положительные;
5)значения аргумента, при которых значения функции отрицательные;
ЗАРАНЕЕ БЛАГОДАРНА)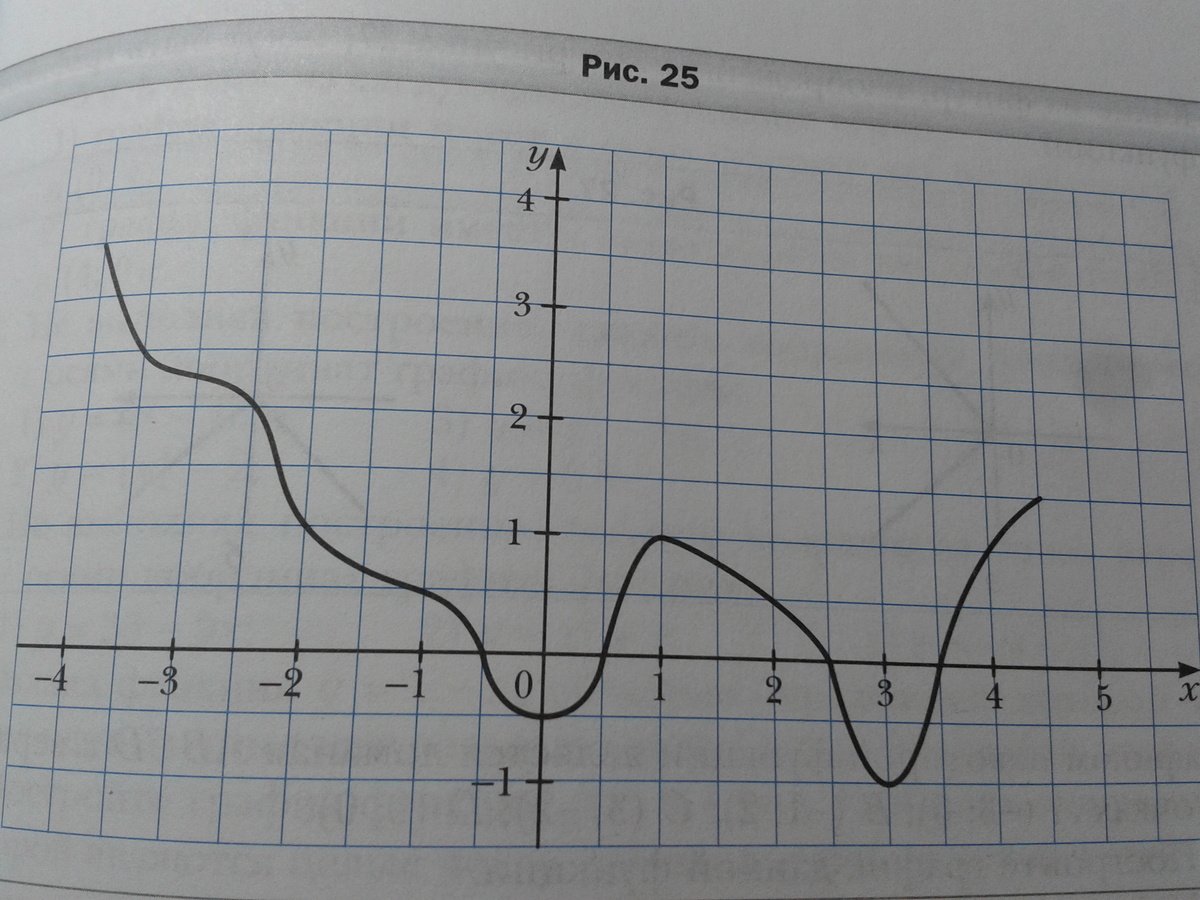
Ответы 1
-
Пользуясь графиком, найдите:1) f(-4), f(-2,5), f(0,5) f(2) - для этого ищем значение на оси абсцисс, проецируем это значение на график и с графика проецируем на ось ординат, где и смотрим значение функции, тогдаf(-4) = 3,5 (для примера смотри рисунок)f(-2,5) = 2f(0,5) = 0f(2) = 0,52) значения х, при которых f(x)=2,5; f(x)=1; f(x)=0. Для этого ищем значение на оси ординат (Оу), проецируем это значение на график и с графика проецируем на ось абсцисс, где и смотрим значение аргумента функции, тогдаf(x)=2,5 ⇒ х = -3,5f(x)=1 ⇒ х = -2 ; х = 1 ; х = 4 (для примера смотри рисунок)f(x)=0 ⇒ х = -0,5 ; х = 0,53) область определения и область значения функции.Тат ка функция не имеет разрыва, то она определена на всей числовой прямой от -4 до 4,5.
Область значения функции находится в интервале от -1 до 3,5. Смотри по оси ординат (Оу)
4) значения аргумента, при которых значения функции положительные.
5) значения аргумента, при которых значения функции отрицательные

-
Автор:
woofie0dgf - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
почему в слове ничтожно пишется и?
-
Предмет:
Русский язык -
Автор:
coreenvatf - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В цехе завода два станка,на которых изготавливают одинаковые детали.На первом станке за 4 ч изготовили 680 деталей,на втором станке за 4 ч изготовили 585 деталей.Какой станок имеет большую производительность?
-
Предмет:
Математика -
Автор:
noah64 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
а)угол COD=84ГРАДУСАМ.Найди величину смежного с ним угла.
б)Во сколько раз угол величеной 18градусов меньше смежного с ним угла?
в)Являются ли смежными углы ABC=56градусов и KMT=124градусов?При каком условии будут смежными углыDOE=75градусов и DOF= 105 градусов ?-
Предмет:
Математика -
Автор:
omar - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Время торможения автомобиля 1 минута. Коэффициент трения 0,02. Определите начальную скорость и тормозной путь автомобиля.
-
Предмет:
Физика -
Автор:
Ángeles0eln - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
