-
Помогите пожалуйста с решением третьего
(ход решения нужен)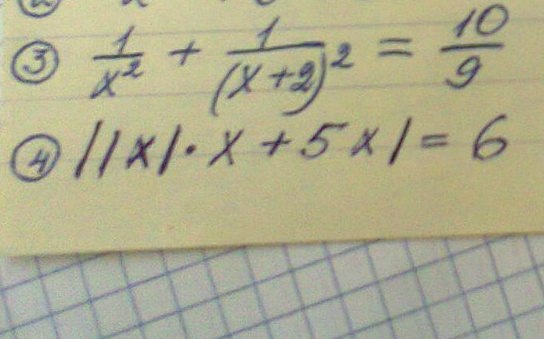
-
Предмет:
Алгебра -
Автор:
bridgerholder - 6 лет назад
-
Ответы 1
-
значит имеем лишь 2 корнях=1 и х=-3проверим решения
-
Автор:
jared29 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Решение какого из данных неравенств изображено на рисунке? 1) x2−36≤0 2) x2−6x≤0 3) x2−6x≥0 4) x2−36≥0
-
сочинение с указательными местоимениями.ПОМОГИТЕ ПОЖАЙЛУСТА!!!!!!!!!
-
Предмет:
Русский язык -
Автор:
jaydin - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- многообразие дикорастущих растений
-
Из всех собранных грибов 2/5 засушили, 5/9 оставшихся засолили, а остальные 28 пожарили. Сколько грибов всего собрали? Какую часть засолили?
решите пожалуйста!!! СРОООЧНОО!!!!! РЕШИТЕ С РЕШЕНИЕМ И ПОЕСНЕНИЕМ :)
-
Предмет:
Математика -
Автор:
mariepkev - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
