-
Решите пожалуйста неравенство с модулями, если можно, то на отдельном листочке)
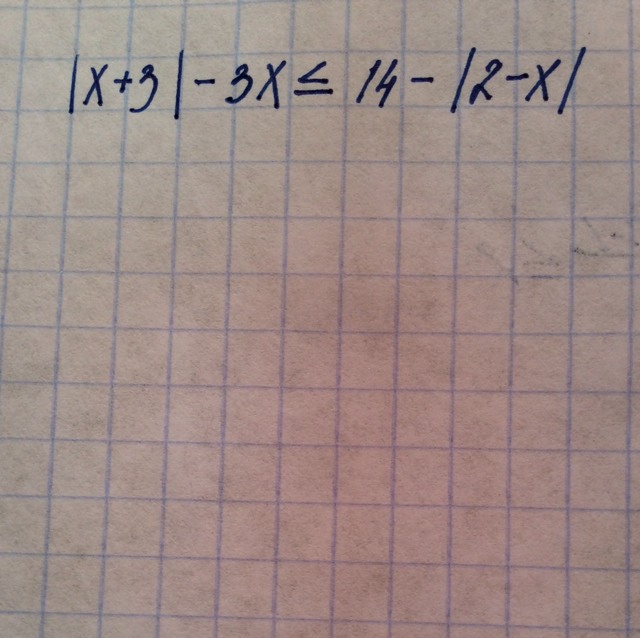
Ответы 2
-
x+3-3x<=14-2-x -x-3-3x<=14+2+xx-3x+x<=14-2-3 -x-3x-x<=14+2+3-x<=9 -5x<=19x>= -9 5x>= -19 x>= -19/5 x>= -3,8<=(меньше или равно)>=(больше или равно)Ответ: х>= -3.8
-
Автор:
rexnkps - 6 лет назад
-
0
-
-
Решать надо отдельно для трех участков координатной оси. Сначала найдем критические точки, там где модули обращаются в ноль. Это точки х=-3 и х=2. эти точки делят числовую ость на 3 интервала Для каждого интервала раскроем модули и потом объединим решения.1) x< -3;-x-3-3x<=14-2+x;5x>=-15;x>= -3; Общих решений в данном интервале нет2) -3<=x<2;x+3-3x<=14-2 +x;3x>=-9;x>=-3 Решением данного интервала будет множество х∈[-3;2);3) x>=2;x+3-3x<=14+2-x;x>=-13. Решением данного интервала будет множество x∈[2;+бесконечность). Объединим все 3 случая и запишем общий ответ для неравенства х∈[-3; +бесконечность)
-
Автор:
annabelwalls - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Реши уравнение (1500+х):80 =70
-
Предмет:
Математика -
Автор:
vargas9cnf - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Два точечных заряда величиной q1=4*10(степень минус 8) Кл и q3=2*10(степень минус 8) Кл находятся на расстоянии 3 м, а заряд величиной q2= -10*10(степень минус 8) Кл поместили в центр отрезка, соединяющего да первых заряда. Определить величину и направление сил, действующих на второй заряд.
-
(5x-3)=(5x+13) решите уравнение
-
Предмет:
Математика -
Автор:
gracelyn - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Благодаря конъюгации и кроссинговеру при образовании гамет происходит а)уменьшение числа негомологичных хромосом вдвое б)увелечение числа сестринских хромосом вдвое в)обмен генетической информацией между сестринскими хромосомами г) обмен генетической информацией между гомологичными хромосомами
-
Предмет:
Биология -
Автор:
scooteripaz - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
