Задать вопрос Регистрация
Помочь другим

  • Найдите наименьшее значение параметра а, при котором уравнение(смотри во вложениях) имеет положительный корень.
    Буква "р" в уравнении это пи.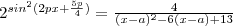

    question img

Ответы 1

  •  Рассмотрим отдельные функций , видно что  у функций  слева максимальное и минимальное значений соответственно будут равны 1 и 2 У функций  y=\frac{4}{(x-a)^2-6(x-a)+13}\\ y'=8x-8a-24=0\\ x=3+a\\ y=\frac{4}{4}=1\\  максимальное значение равна 1.Откуда видно что они могут пересекаться только в точке равным 1    2^{sin^2(2\pi*x+\frac{5\pi}{4})}=2^0\\ x=\frac{k}{2}-\frac{1}{8}\\ x \geq 0\\ k=\frac{1}{4}\\ x=0\\\\  Тогда уравнение в правой части будет  (x-a)^2-6(x-a)+9=0\\ x^2-2ax+a^2-6x+6a+9=0\\ x^2-x(2a+6)+(a+3)^2=0\\ D=4(a+3)^2-4(a+3)^2 = 0\\ x=(2a+6)/2=a+3 \\ a=-3  то есть при   a=-3 

    • Автор:

      matilde
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years