-
Ребят, помогите пожалуйста, целый день не могу решить его, ответ должен получиться: ab/(a+b)^2
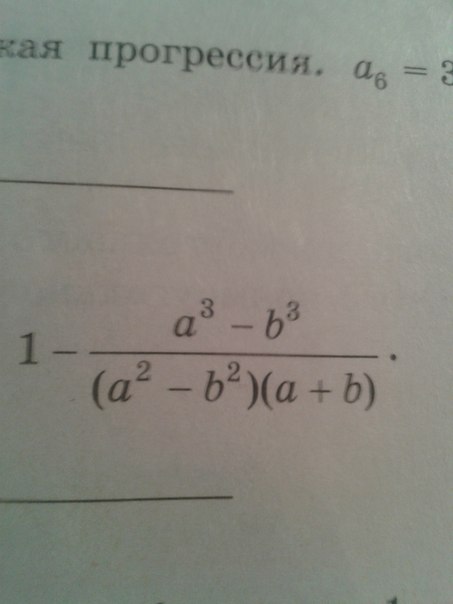
Ответы 2
-
спрашивайте, где не понятно)
-
Автор:
naima - 5 лет назад
-
0
-
-
1)применяем формулы к знаменателю:1-[ (a^3-b^3) / (a-b)(a+b)(a+b)]2)применяем формулы к числителю:1-[ (a-b)(a^2+ab+b^2) / (a-b)(a+b)^2]3) сокращаем дробь:1-[ (a^2+ab+b^2) / (a+b)^2]4) приводим к общему знаменателю:[(a+b)^2-(a^2+ab+b^2)] / (a+b)^25) раскрываем скобки:[a^2+ab+b^2-a^2-ab-b^2]/ (a+b)^2==ab/(a+b)^2
-
Автор:
doritoseus - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
4b в кубе-b
Разложите на множители-
Предмет:
Алгебра -
Автор:
lindsaya8h0 - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
як по-іншому називають Мадагаскар?
-
Предмет:
География -
Автор:
georgereese - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
укажите области применения серы:
а) получение резины,
б) производство спичек,
в) получение серной кислоты,
г) обеззараживание воды -
Напишите недостатки использования интернета (на английском).
-
Предмет:
Английский язык -
Автор:
bambisjfe - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
