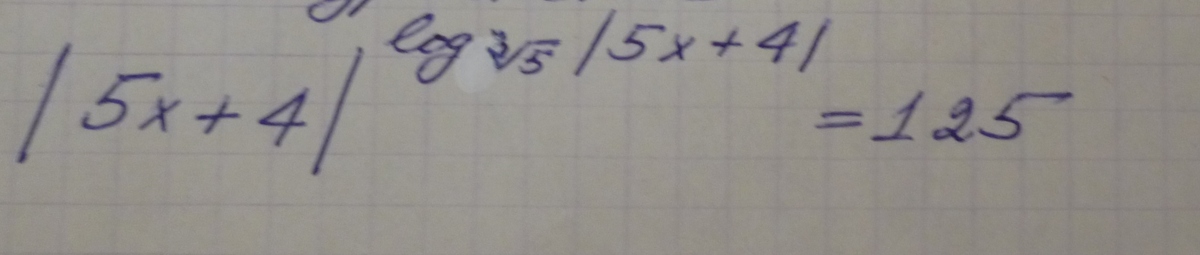Ответы 1
-
|5x+4|>0,
[5x+4>0, -(5x+4)>0;
[x>-4/5, x<-4/5;
x≠-4/5;
[
[
[
[
[
[
[
[
[ 5x=-19/5, 5x=-21/5, 5x=1, 5x=-9;
[ x=-19/25, x=-21/25, x=1/5, 5x=-9/5;
-
Автор:
tootsiexyeq - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Помогите решить уравнение: (x^2 - 9)^2 - 8(x^2 - 9) + 7 = 0
-
Упростите выражения: а) -2х(1-х)+(2х-3)(х-1)
б)4(1+3у)²-24х в)(х+4)(х-4)-(х-3)² г)(а-1)²(2+3а)²
д)(3-b)²(3b+2)² -
выразите из формул все величины:
А=Fs - формула работы
N=A/t - формула мощностиM=FL - момент силы
η=А полезная /Aзатраченная - КПД
Eпотенциальная=mgh - потенциальная энергия
Eкинетическая=mv^2/2 - кинетическая энергия-
Предмет:
Физика -
Автор:
dukebenson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Пончик,Незнайка и Цветик участвовали в конкурсе сладкоежек.Незнайка съел 51 пончик,что составило 34% всех пончиков.Сколько пончиков досталось Цветику,если Пончик съел 50% сладостей?
-
Предмет:
Математика -
Автор:
earlbb3d - 6 лет назад
-
Ответов:
1 -
Смотреть
-