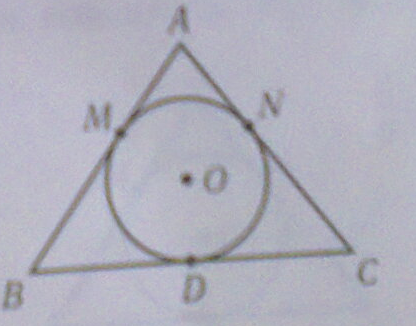
дано треугольник abc ab=ac=15 см периметр треугольника = 48 см m n d - точки касания сторон и вписанной окружности найди а)длины отрезков bm и am -б) радиус вписанной окружности

Треугольник равнобедренный по условию задачи. 

Для ее решения нужно вспомнить теорему об отрезках касательных к окружности из одной точки. Они равны.

ВС делится точкой касания окружности на 2 равные части. 

ВС=48-2*15=18

ВМ=ВD=9 cм

AM=AB-BM=15-9

AM=6 cм

Радиус вписанной окружности находят по формуле

r=S:p, где S- площадь  треугольника, а p - его полупериметр.

Чтобы найти площадь, нужно знать высоту. Она равна 12( вычислите по теореме Пифагора или вспомните, что если провести из вершины А высоту, получится египетский треугольник с отношением сторон 3:4:5)

S=12*18:2=108 см² 

р=48:2=24

r=108:24=4,5 см