Задать вопрос Регистрация
Помочь другим

  • Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и фор­му­ла­ми, ко­то­рые их за­да­ют.
    1) у=х^2+3x+3
    2) y=-x^2-3x-3
    3) y=x^2-3x+3
    4) y=-x^2+3x-3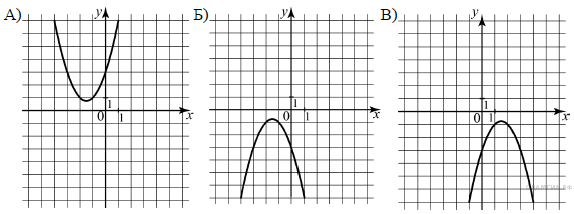

    question img

Ответы 1

  • Даны 4 уравнения параболы и три графика параболы.Если коэффициент перед x² больше нуля, то ветви параболы направлены вверх, меньше нуля - направлены вниз. Отсюда следует, что графику функции А соответствует либо формула 1, либо формула 3.Чтобы решить этот вопрос, для всех формул выделим полный квадрат:1) y = x^2+3x+3 = x^2+2* \frac{3}{2}*x+ (\frac{3}{2})^2+ \frac{3}{4} =(x+ \frac{3}{2} )^2+ \frac{3}{4} Значит, вершина параболы находится в точке (-1,5; 0,75), а ветви параболы направлены вверх, что соответствует графику А.2) y = -x^2-3x-3 = -x^2-2* \frac{3}{2}*x- (\frac{3}{2})^2- \frac{3}{4} = \\ \\ = -(x^2 +2* \frac{3}{2}*x+ (\frac{3}{2})^2) - \frac{3}{4}= -(x+ \frac{3}{2} )^2 - \frac{3}{4}Значит, вершина параболы находится в точке (-1,5; -0,75), а ветви параболы направлены вниз, что соответствует графику Б.3) y = x^2-3x+3 = x^2-2* \frac{3}{2}*x+ (-\frac{3}{2})^2+ \frac{3}{4} =(x- \frac{3}{2} )^2+ \frac{3}{4}Значит, вершина параболы находится в точке (1,5; 0,75), а ветви параболы направлены вверх, что не соответствует ни одному графику.4) y = -x^2+3x-3 = -x^2-2* \frac{-3}{2}*x- (\frac{-3}{2})^2- \frac{3}{4} = \\ \\ = -(x^2 +2* \frac{-3}{2}*x+ (\frac{-3}{2})^2) - \frac{3}{4}= -(x- \frac{3}{2} )^2 - \frac{3}{4}Значит, вершина параболы находится в точке (1,5; -0,75), а ветви направлены вниз, что соответствует графику В.

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years