-
Очень хочется разобраться. Помогите, пожалуйста!:) Алгебра, 9 класс.
Найдите все такие пары чисел (x, y), что выражение (на картинке) принимает минимальное значение. Спасибо большое :))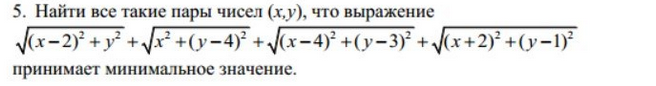
-
Предмет:
Алгебра -
Автор:
concepción - 6 лет назад
-
Ответы 1
-
Можно задачу интерпретировать в геометрию . Сами выражения
представляют собой длины отрезков . Если задачу рассматривать с геометрической точки зрения , получим некие точки , обозначим
,и некая точка
. Требуется найти такую точку что сумма расстояний от точки
, к вершинам
была минимальной. Заметим что если обозначить в координатной плоскости
, получим параллелограмм
. Длины сторон
, все по той же формуле
. Видно что минимальное значение будет , это точка пересечения диагоналей. Точка
есть точка пересечения диагоналей. Так как в точке пересечения диагонали делятся пополам. То получим
\
Для проверки можно положить
Рассмотреть функцию , находя производную приравняв к 0 , получим
Ответ
минимальное значение равно
-
Автор:
londondixon - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Расположи по каким группам относятся эти названия летних месяцев.
Летние месяца и их названия:
Июнь- червень, хлеборост, светозар, разноцвет, земляничник, скопидом.
Июль - липень , страдник,сеозарник макушка лета, сеностав,жарник,грозовик,грозник.
Август- серпень,жнивень, разносол,густоед,хлебосол,собериха,зорничник
Группы:
а) с явлениями неживой природы -.....
в) с явлениями живой природы -....
б) с трудом людей -......-
Предмет:
Обществознание -
Автор:
harry12 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Сочинение про спорт на казахском языке предложений 4 не больше
-
Предмет:
Қазақ тiлi -
Автор:
ashtynriddle - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- y=3x-x^3-5 срочно нужно решить!
-
Расположи по каким группам относятся эти названия летних месяцев.
Летние месяца и их названия:
Июнь- червень, хлеборост, светозар, разноцвет, земляничник, скопидом.
Июль - липень , страдник,сеозарник макушка лета, сеностав,жарник,грозовик,грозник.
Август- серпень,жнивень, разносол,густоед,хлебосол,собериха,зорничник
Группы:
а) с явлениями неживой природы -.....
в) с явлениями живой природы -....
б) с трудом людей -......-
Предмет:
Русский язык -
Автор:
ivan25 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
