Задать вопрос Регистрация
Помочь другим

  • Помогите решить плииз с объяснением, завтра уже зно, не знаю как это решить((

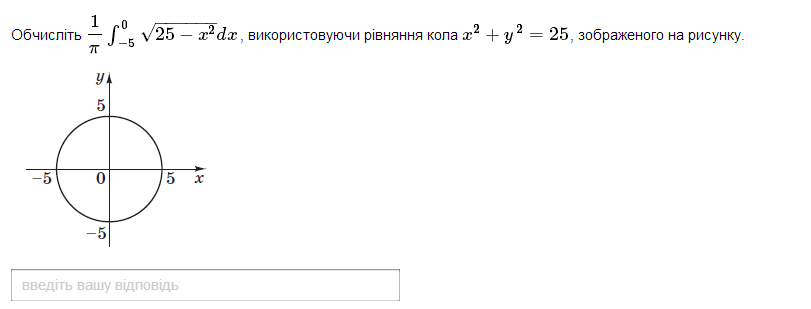
    question img

Ответы 1

  • \frac{1}{\pi }\int _{-5}^0\sqrt{25-x^2}dx=\\\\=[x=5sint,dx=5costdt,x_1=-5,t_1=-\frac{\pi}{2},x_2=0,t_2=0]=\\\\=\frac{1}{\pi }\int _{-\frac{\pi}{2}}^0\sqrt{25-25sin^2t}\cdot 5costdt=\frac{1}{\pi }\int _{-\frac{\pi}{2}}^0\sqrt{25(1-cos^2t)}\cdot 5costdt=\\\\=\frac{1}{\pi }\int _{-\frac{\pi}{2}}^025cos^2tdt=\frac{25}{\pi }\int _{-\frac{\pi}{2}}^0\frac{1+cos2t}{2}dt=\frac{25}{2\pi }(t+\frac{1}{2}sin2t)|_{-\frac{\pi}{2}}^0=\\\\=\frac{25}{2\pi }(\frac{\pi}{2}-\frac{1}{2}\cdot 0)=\frac{25}{4}=6,25Если использовать чертёж. то определённый интеграл выражает площадь части круга, лежащего во 2 четверти, то есть площадь четверти круга с радиусом R=5.S=ПR²=25П,  S/4=25П/4(1/П)*(S/4)=25/4=6,25

    • Автор:

      bumpkin
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years