-
Очень легкое задание на лимит....так хочется спать, что смотрю в книгу и ничего не вижу(((Последнее задание осталось
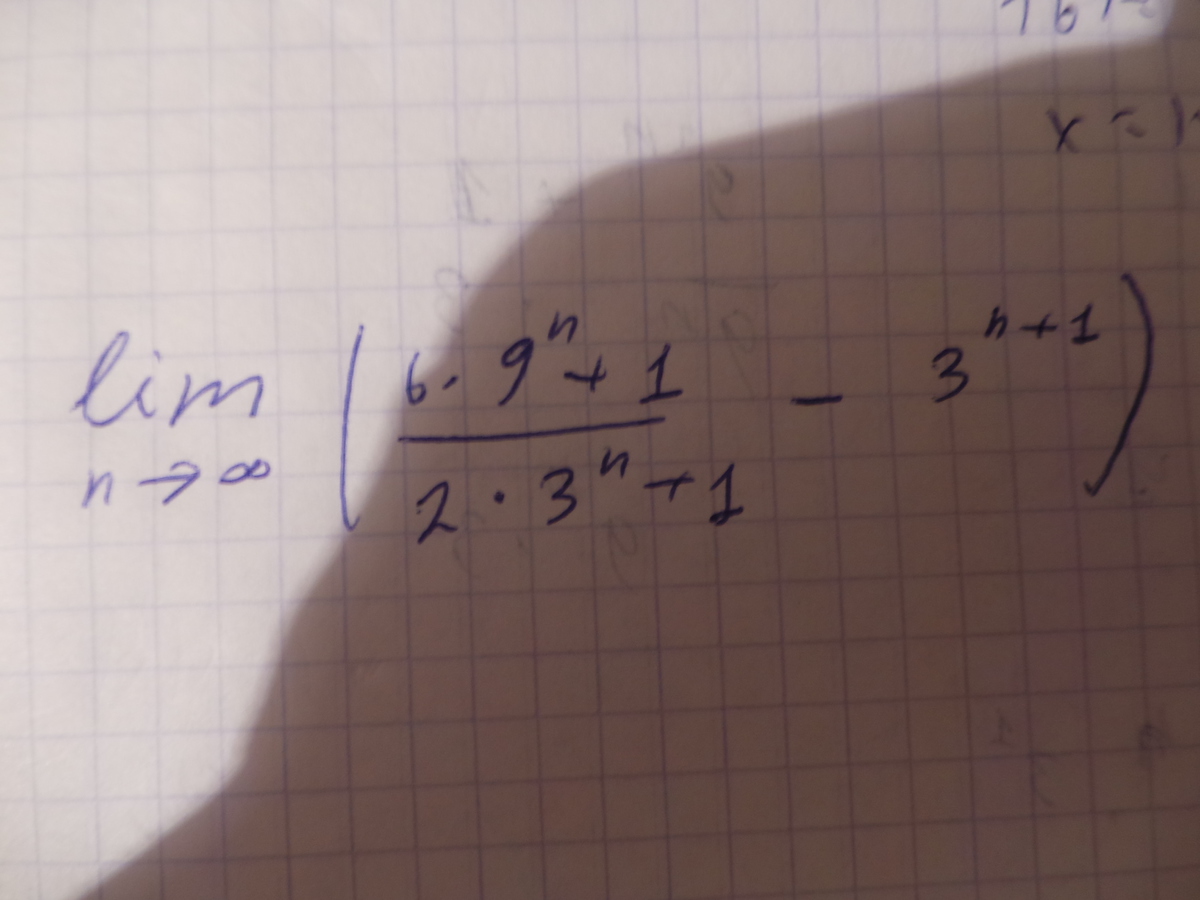
-
Предмет:
Алгебра -
Автор:
blakemorales - 6 лет назад
-
Ответы 3
-
Оно действительно не сложное, просто объемное.
-
Автор:
deannavl3l - 6 лет назад
-
0
-
-
Уровень сложности задачи индивидуален. Одним одно легко, другим - другое, третьим все трудно.... а кому-то и просто лень.
-
Автор:
violasg72 - 6 лет назад
-
0
-
-
-
Автор:
buds - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Решите уравнение, предварительно упростив его левую часть. а)10,15-(8,26-x)=-4 3/5 И. б) 9,3-(|x-4|-3 2/5)=5
-
Предмет:
Математика -
Автор:
liviab5g7 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
- Чему равна производная (cos x)'?
-
Каковы пределы изменения функции если х меняется от -5 до 5
y=-3x^2+17
-
Предмет:
Алгебра -
Автор:
heisenbergwimn - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Конкурирующий магазин спортивных товаров расположен в торговом центре, а ваш, более крупный магазин, торгующий аналогичными товарами, - в спальном районе. Как вы построите работу своего магазина, чтобы лишить конкурента его преимущества в размещении?
How much to ban the user?
1 hour
1 day
100 years
