Найдите наибольшее значение функцииy=2^(-37-12x-x^2)Для наглядности прикреплю картинку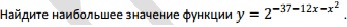

Ответы 4

Если не видно формул, обновите страницу.
- Автор:
  watson
- 5 лет назад
- 0
Если есть вопросы по решению, их тоже можно смело задавать.
- Автор:
  jasperelaj
- 5 лет назад
- 0
Большое спасибо! Вопросов нет, всё понятно.
- Автор:
  balduinoward
- 5 лет назад
- 0
$y = 2^{-37 - 12x - x^2} = 2^{-(x^2 + 12x + 37)}$ $f = x^2 + 12x + 37$ парабола, ветви которой направленны вверх. $D = 144 - 4*37 = 144 - 148 = -4 < 0 \ \Rightarrow$ корней нет, вершина параболы лежит выше оси абсцисс. При большем значении принимаемом параболой f получим меньшее значение исходной функции y. $2^{-x} > 2^{-(x+1)}, \ x > 0$ Минимальное значение этой параболы соответствует её вершине. Найдём абсциссу и ординату вершины и подставим в исходное уравнение. $x_v = -\frac{12}{2} = -6\\\\ y_v = (-6)^2 + 12*(-6) + 37 = 36 - 72 + 37 = 1\\\\ f(x_v) = 2^{-y_v} = 2^{-1} = \boxed{0.5}$
- Автор:
  jenkins
- 5 лет назад
- 0
Добавить свой ответ