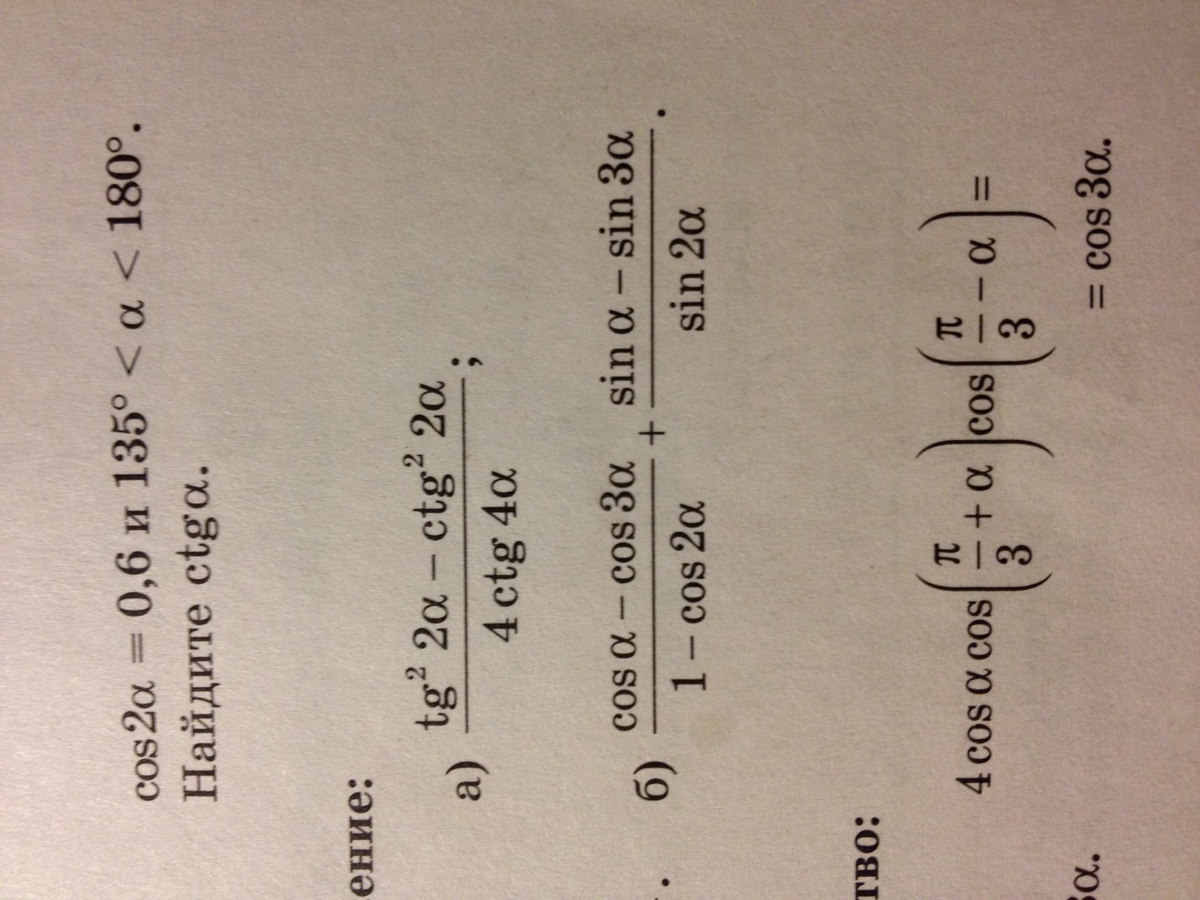Ответы 2
-
1)=[(sin^4(2a)-cos^4(2a)]sin4a/sin²2a*cos²2a*4cos4a==-2cos4a*sin4a*4/sin²4a*4cos4a=-2/sin4a2)=2sinasin2a/2sin²a - 2sinacos2a/2sinacosa=sin2a/sina - cos2a/cosa==(sin2acosa-cos2asina)/sinacosa=sina/sinacosa=1/cosa
-
Автор:
abigailaduh - 5 лет назад
-
0
-
-
-
Автор:
brysonojdk - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Напишите пожалуйста мнения авторитетных историков на Николая 2 (Романова)
пожалуйста!! - вычислите массовые доли каждого элемента в следующих соединениях а)МgO b)CO2 h) Al2O3 k) KMnO4
-
какие из явлений послужили основой для предположения об атомно-молекулярном строении вещества:1) испарение жидкости ;2) распространение запахов ;3) броуновское движение?
А. только 1
б.только 2
в. только 3
г. 1,2 и 3
-
Предмет:
Физика -
Автор:
rockethruc - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Пожалуйста помогите!!!
Тимур нужно купить 5 литров молока. Один пакет молока объём 1 литр стоит 52 рубля. Один пакет молока объём 2 литра стоит 97 рублей. Кроме того, в магазине проходит акция: три литровых пакета молока продаются по цене двух таких же пакетов. Какую наименьшую сумму в рублях потратит Тимур на Покупку? Ответ поясните. Решение-
Предмет:
Алгебра -
Автор:
jellyshaffer - 5 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years