Задать вопрос Регистрация
Помочь другим

  • Вычисли площади фигур ограниченных линиями см рис
    Построить заданные фигуры

    Значения n=29, m=7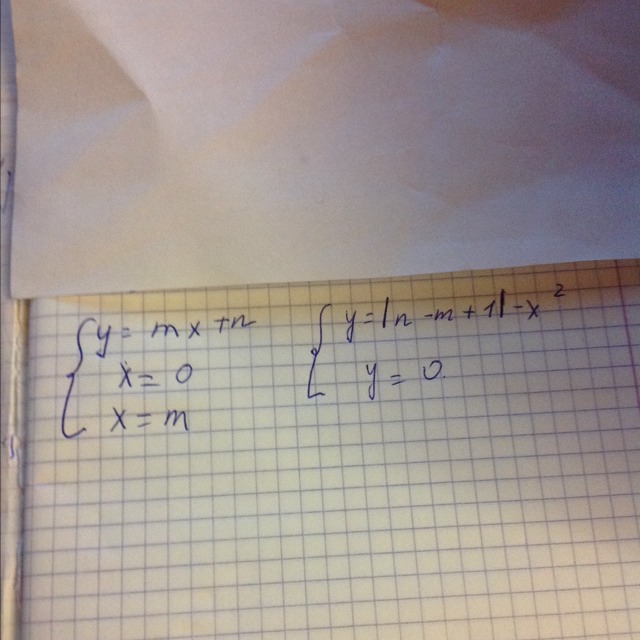

    question img

Ответы 1

  • 1) у=0 - ось ох     х=7 - прямая ||  оси оу     у=7х+29 - прямая пересекающая ось ох в точке  (-29/7; 0)    и ось оу в точке (0; 29)  Искомая площадь - площадь треугольника АВС  Можно найти как половина произведения катетов Один катет по оси ох    7 - (-29/7)=78/7  Второй по оси у  - ордината прямой  у=7х+29  при х=7  у=7·7+29=78S= \frac{1}{2}\cdot 78 \cdot \frac{78}{7}= \frac{3042}{7}=434 \frac{4}{7} илиS= \int\limits^{7}_{- \frac{29}{7}} {(7x+29)} \, dx=(7 \frac{ x^{2} }{2} +29x)| _{- \frac{29}{7} } ^{7}= \\ =7\cdot \frac{7 ^{2} }{2}+29\cdot 7 - (7\cdot \frac{(- \frac{29}{7}) ^{2} }{2}+29\cdot(- \frac{29}{7}))= \frac{749}{2} -( \frac{841}{14}- \frac{841}{7} )= \\ = \frac{5243}{14}+ \frac{841}{14}= \frac{6084}{14}= \frac{3042}{7} =434 \frac{4}{7} 2) y=|n-m+1|-x²   при  n=29,    m=7    принимает вид     у=|29-7+1|-x²      или     у=23-х²Графиком является парабола, ветви которой направлены вниз, парабола имеет вершину в точке (0;23) и пересекает ось ох в точках (-√23; 0)  и (√23; 0)  у=0 - уравнение оси ох Искомая площадь - площадь под параболой, снизу ограничена осью охS= \int\limits^{ \sqrt{23}} _{- \sqrt{23}} {(23- x^{2}) } \, dx =2 \int\limits^ {\sqrt{23}} _0 {(23- x^{2} )} \, dx =2\cdot(23x- \frac{ x^{3} }{3})| _{0} ^{ \sqrt{23} }= \\ =2\cdot (23 \sqrt{23}- \frac{( \sqrt{23}) ^{3} }{3})= =46 \sqrt{23}- \frac{46 \sqrt{23} }{3}= \frac{92 \sqrt{23} }{3}
    answer img

    • Автор:

      jaylaxxis
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years