Найти предел, Lim (x-->+бесконечность) (9*x^2+1)^(1/2)-3*x Только с решением! Иначе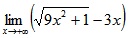

Ответы 3

не совсем ясно, если учесть, что я еще не проходил пределы)
- Автор:
  montana
- 5 лет назад
- 0
При х-->+бесконечность подкоренное выражение -->3х. 3х-3х =0.
- Автор:
  aldoroberson
- 5 лет назад
- 0
$\lim_{x \to \infty} ( \sqrt{9 x^{2} +1}-3x )= \lim_{x \to \infty} \frac{(\sqrt{9 x^{2} +1}-3x)(\sqrt{9 x^{2} +1}+3x)}{\sqrt{9 x^{2} +1}+3x} = \\ =\lim_{x \to \infty} \frac{9 x^{2} +1-9 x^{2} }{\sqrt{9 x^{2} +1}+3x} =\lim_{x \to \infty} \frac{1}{\sqrt{9 x^{2} +1}+3x}= \\ =\lim_{x \to \infty} \frac{1/x}{\sqrt{9 x^{2}/ x^{2} +1/ x^{2} }+3x/x}=0. \\ ( \frac{1}{x} \to 0, \ x \to\infty) \\ \\ \lim_{x \to \infty} ( \sqrt{9 x^{2} +1}-3x )=0.$
- Автор:
  josue606
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы