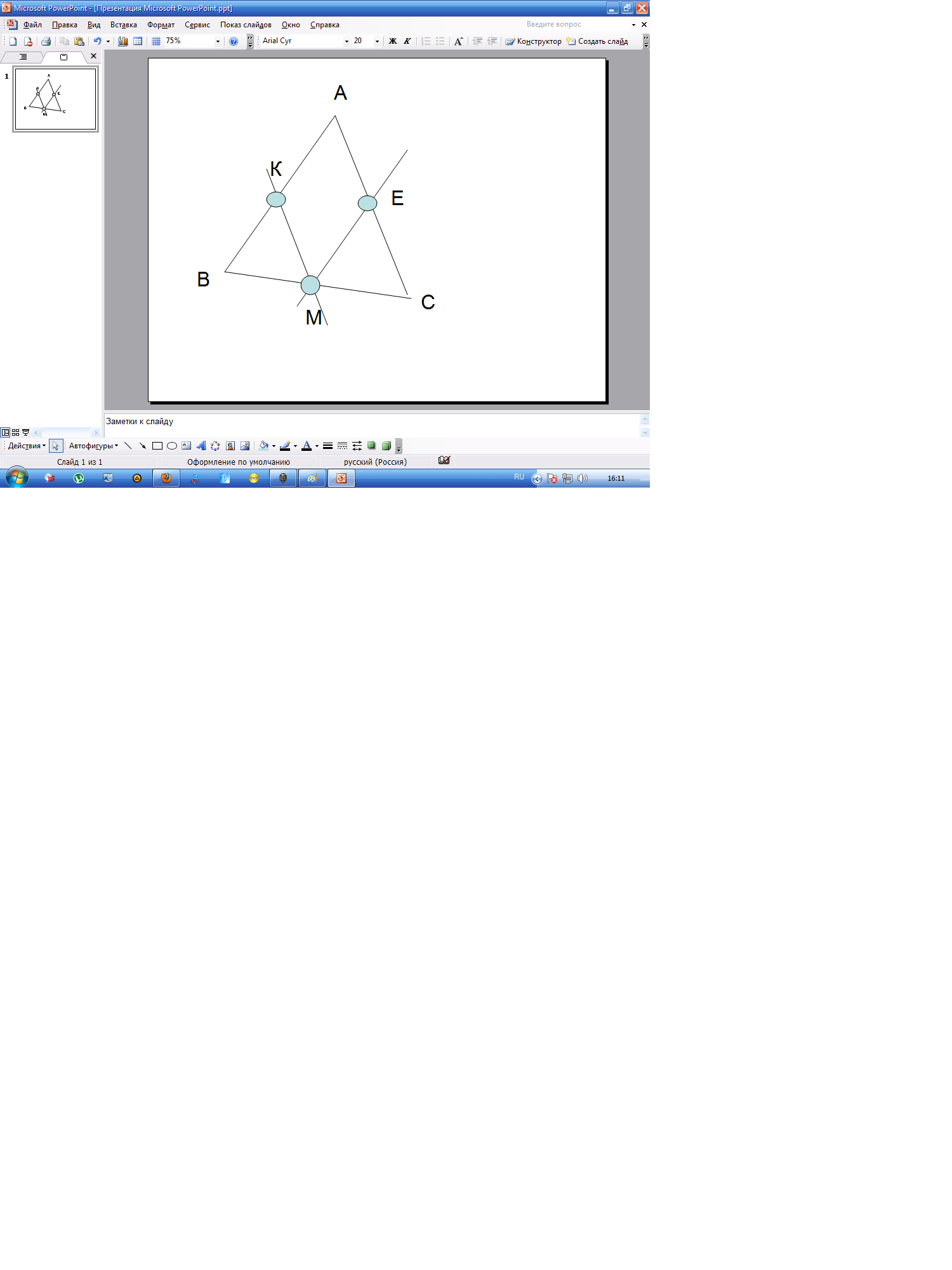
Через точку М, лежащую на стороне ВС треугольника АВС, проведены прямые, параллельно сторонам АВ и АС. Известно, что площади треугольников, отсекаемых этими прямыми от треугольника АВС, равны S1 и S2. Найти площадь треугольника АВС

 

РЕШЕНИЕ

площадь ΔABC =S

площадь ΔEMC =S1

площадь ΔKBM =S2

AKME - параллелограмм

S(AKME)=AK*AE*sinA  =S-(S1+S2)

ΔABC ~ΔEMC -подобные

 AB/EM =k1 -коэффициент подобия

S/S1 =k1^2=(AB/EM)^2 -площади пропорциональны

ΔABC ~ΔKBM -подобные

 AC/KM =k2 -коэффициент подобия

S/S2 =k2^2=(AC/KM)^2 -площади пропорциональны

S/S1=(AB/EM)^2 (1)

S/S2=(AC/KM)^2 (2)

умножим (1) на (2)

S/S1* S/S2=(AB/EM)^2*(AC/KM)^2

S/S1* S/S2=(AB/EM*AC/KM)^2

S/S1* S/S2=((AB*AC)/(EM*KM))^2

<A=<KME - это параллелограмм

умножим ЧИСЛИТЕЛЬ и ЗНАМЕНАТЕЛЬ правой части выражения на sinA

S/S1* S/S2=((AB*AC*sinA)/(EM*KM*sinA))^2

(AB*AC*sinA)=2S -формула площади треугольника

(EM*KM*sinA)=S-(S1+S2)) -формула  площади параллелограмма

S/S1* S/S2=(2S/(S-(S1+S2)))^2

S^2/(S1*S2)=4S^2/(S-(S1+S2))^2

1/(S1*S2)=4/(S-(S1+S2))^2

(S-(S1+S2))^2=4 (S1*S2)

возьмем квадратный корень из правой и левой части

√ (S-(S1+S2))^2 =√4 (S1*S2)

S-(S1+S2) =2√ (S1*S2)

S=2√ (S1*S2)+(S1+S2)

S=(√S1)^2+ 2√ (S1*S2)+(√S2)^2 -формула квадрат суммы чисел

S=( √S1+√S2)^2

Ответ  площадь треугольника АВС S= ( √S1+√S2)^2