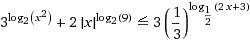Помогите решить , я не понимаю очень срочно

3^(log2(x^2))+2*IxI^(log2(9)<=3*(1/3)^(log1/2(2x+3))ОДЗ: x≠0; 2x+3>0⇒x>-3/2Применяемые формулы: a^(m/n)=(a^m)^(1/n); (a^m)^n=a^(m*n)Все формулы справедливы как справа налево, так и слева направоa^(loga(b)=b - основное логарифмическое тождествоЧитается: a в степени логарифм b по основанию a равен  bФормулы перехода к другому основанию:loga(b)=logc(b): logc(a); loga(b)=1:logb(a), где b>0, c>0, c≠1Перейдем в log2(x^2) к основанию 3, чтобы воспользоваться основным тригонометрическим тождеством log2(x^2)=log3(x^2):log3(2)⇒3^(log2(x^2))=3^(log3(x^2)/log3(2))=(3^(log3(x^2))^(1/log3(2))=(3^(log3(x^2))^(log2(3)=(x^2)^(log2(3)(IxI)^(log2(9))=(IxI)^(log2(3^2))=(IxI)^(2log2(3))=(IxI^2)^(log2(3))=(x^2)^(log2(3))(IxI)^2=x^2(x^2)^(log2(3)+2(x^2)^(log2(3)=3*(x^2)^(log2(3) - выражение в левой части нер-ваЗаймемся правой частьюВ показателе степени перейдем к основанию 2:log1/2(2x+3)=log2(2x+3):log2(1/2)log2(1/2)=-1, так как 2(-1)=1/2^1=1/2 log1/2(2x+3)=log2(2x+3):(-1)=-log2(2x+3)Полезна формула a^(-n)=1/a^n Из выше сказанного имеем:(1/3)^(log1/2(2x+3))=(3^(-1))^(-log2(2x+3))=3^(log2(2x+3))Перейдем в log2(2x+3) к основанию 3, чтобы воспользоваться основным тригонометрическим тождеством log2(2x+3)=log3(2x+3):log3(2)3^(log2(2x+3))=3^(log3(2x+3):log3(2))=(3^(log3(2x+3))^(1/log3(2)==(3^(log3(2x+3))^(log2(3)=(2x+3)^(log2(3)Итак, справа получаем выражение 3*(2x+3)^(log2(3)Неравенство имеет вид3*(x^2)^(log2(3)<=3*(2x+3)^(log2(3)⇒(x^2)^(log2(3)<=(2x+3)^(log2(3)log2(3)>1Рассмотрим значения левой и правой частей в области определения (-3/2;+∞)Нужно определить, где каждое основание больше 1 и где меньше 1. Это нужно для дальнейшего сравнения.x^2<=1, если -1<=x<=1x∈(-3/2;-1)⇒x^2>1x∈[-1;0)∨(0;1]⇒x^2<=1x∈(1;+∞)⇒x^2>12x+3>=1⇒2x>-2⇒x>=-1x∈(-3/2;-1)⇒2x+3<1x∈[-1;0)∨(0;1]⇒2x+3>=1x∈(1;+∞)⇒2x+3>1Теперь проведем сравнение  в каждом интервале1) x∈(-3/2;-1)x^2>1; (2x+3)<1⇒(x^2)^(log2(3))>(2x+3)^(lo2(3))В этом интервале решений нет2) x∈[-1;0)∨(0;1]x^2<=1; 2x+3>=1⇒(x^2)^(log2(3))<=(2x+3)^(log2(3))Каждое значение из этого интервала является решением3)x∉(1;+∞)x^2>=1; 2x+3>=1Неравенство будет верным, если x^2<=2x+3⇒x^2-2x-3<=0Решим уравнение: x^2-2x-3=0. По теореме Виетта x1+x2=2; x1*x2=-3⇒x1=3; x2=-1. Эти значения разбивают числовую ось на 3 промежутка:(-∞;-1); [-1;3]; (3;+∞)По методу интервалов в крайнем справа будет +, дальше идет чередование.x^2-2x-3<=0⇒x∈[-1;3], а в нашем интервале x∈(1;3]Объединяя 2) и 3) получаем x∈[-1;0)∨(0;3]