-
СРОЧНО
Помогите пожалуйста вычислить неопределенный интеграл под №2 и определенный №4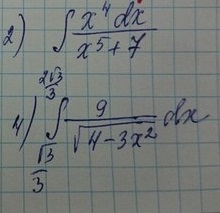
Ответы 1
-
-
Автор:
chuckyaustin - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
решите срочно 2 целых шесть седьмых дробная черта 3 целых три четырнадцатых
-
Предмет:
Математика -
Автор:
tristanreyes - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
в каком направлении вернутся туристы если уходили они на восток
-
Предмет:
Другие предметы -
Автор:
bubbaf71m - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
По расчетам ньютона два шара диаметром по 30 см, расположенный на расстоянии 0,6 см, сойдутся под действием силы взаимного притяжения через месяц после
начала движения (расчет производится при отсутствии внешнего сопротивления).Плотность шаров ньютон брал равной средней плотности земли: p 5*10^3 кг/м^3 . (силу тяготения считать постоянной). прав ли ученый?-
Предмет:
Физика -
Автор:
geovannimveu - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
сделайте подборку рекомендаций по обеспечению безопасного проезда по железной дороге
-
Предмет:
Другие предметы -
Автор:
hobbesbowers - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
