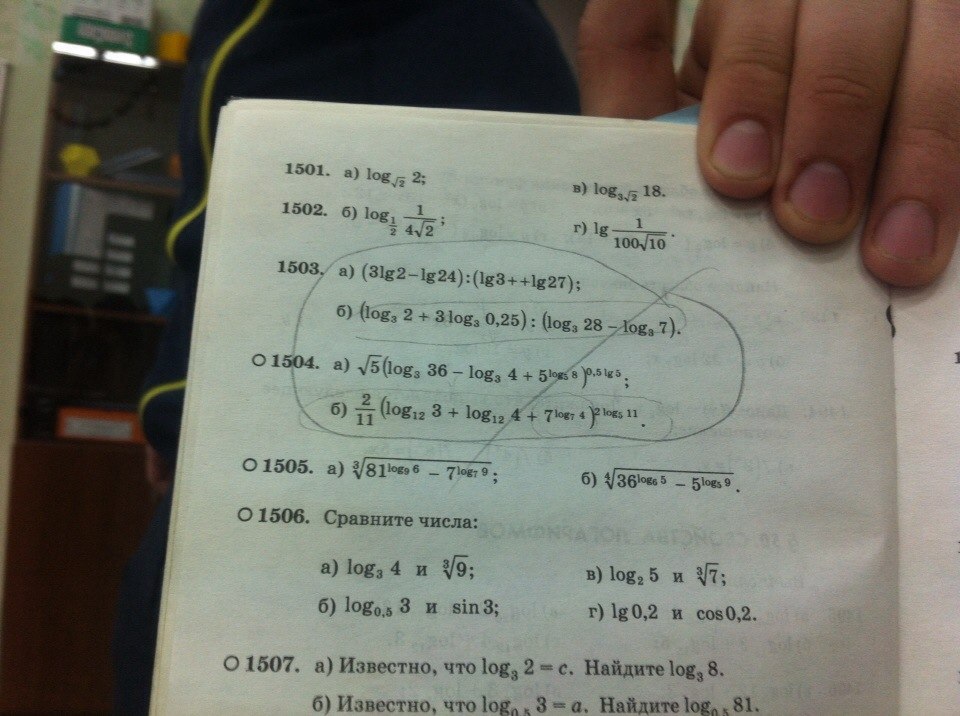Ответы 2
-
огромное спасибо
-
Автор:
nakita - 6 лет назад
-
0
-
-
-
Автор:
evelingmal - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Привет всем помагите пожалуйста по русскому 3класс срочно 330 уп
-
Предмет:
Русский язык -
Автор:
ariel1 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
решите уравнение 30х-12х=126
-
Предмет:
Математика -
Автор:
bam-bamnguyen - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
найдите значение выражения 3х+8х-х при х-46
-
Предмет:
Математика -
Автор:
elvistjf5 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
вспомните или подберите по славорю пословицы, в состав которых входит числительное семь?? Помогите срочноо
-
Предмет:
Математика -
Автор:
nikhilm9tr - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years