lim 2x^2-x^2 поделить на 4-х^2 (когда Х устремляеться к 2-м)

lim 2x^2-x^2 поделить на 4-х^2 (когда Х устремляеться к 2-м)
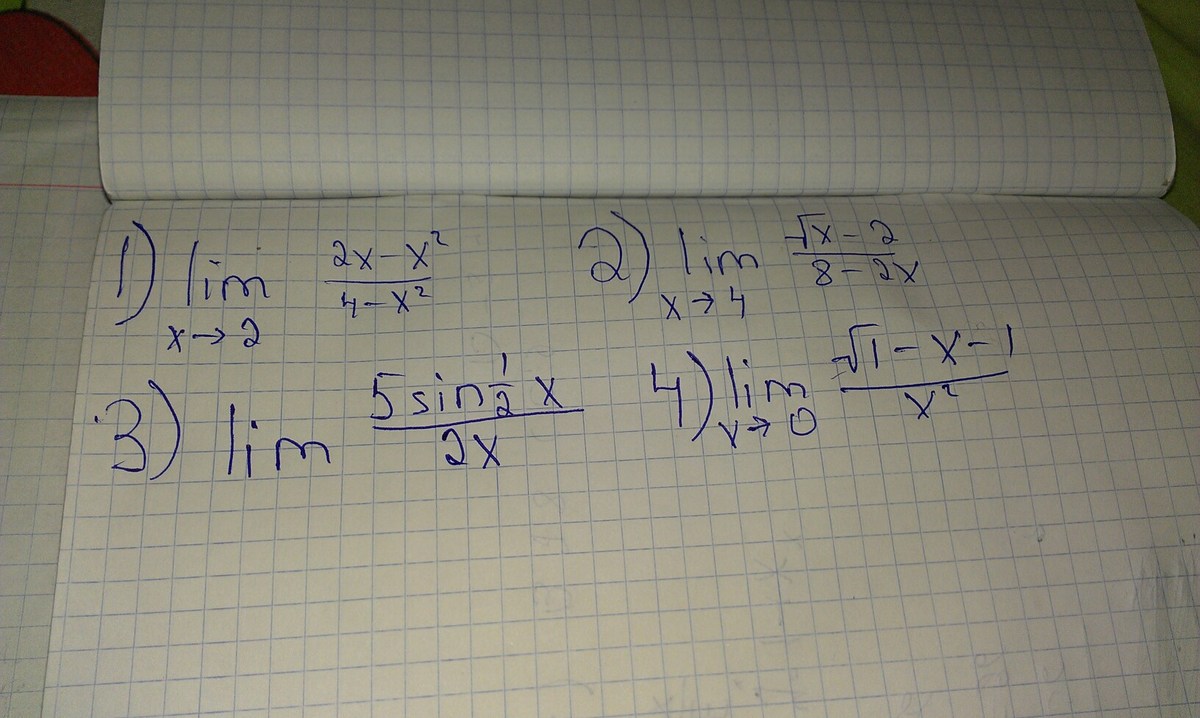
- Предмет:
  Алгебра
- Автор:
  stanleykj1l
- 6 лет назад

Ответы 2

lim_{x->2} (2x-x^2)/(4-x^2) = lim_{x->2} x(2-x)/((2+x)(2-x)) = lim_{x->2} x/(2+x) = 2/(2+2) = 1/2,

lim_{x->4} (√x-2)/(8-2x) = lim_{x->4} (√x-2)/(-2(x-4)) = lim_{x->4} (√x-2)/(-2(√x+2)(√x-2)) = lim_{x->4} -1/(2(√x+2)) = -1/(2(√4+2) = -1/8;

lim_{x->0} (√1-x-1)/x^2 = lim_{x->0} -x/x^2 = lim_{x->0} -1/x = -∞,

lim_{x->0} 5sin(x/2)/(2x) = lim_{x->0} 5sin(x/2)/(4*x/2) = 5/4 lim_{x->0} sin(x/2)/(x/2) =5/4 *1 = 5/4.
- Автор:
  english90
- 6 лет назад
- 0
$lim_{x->2} \frac{2x^2-2x^2}{4-x^2}=lim_{x->2} \frac{0}{4-x^2}=lim_{x->2} 0=0$

вложение

$lim_{x->2} \frac{2x-x^2}{4-x^2}=lim_{x->2} \frac{x(2-x)}{(2-x)(2+x)}=lim_{x->2} \frac{x}{2+x}=\frac{2}{2+2}=0.5$

$lim_{x->4} \frac{\sqrt{x}-2}{8-2x}=\\ lim_{x->4} \frac{\sqrt{x}-2}{2(4-x)}=\\ lim_{x->4} \frac{\sqrt{x}-2}{2(2-\sqrt{x})(2+\sqrt{x})}=\\ lim_{x->4} \frac{1}{-2(2+\sqrt{x})}=\\ \frac{1}{-2*(2+\sqrt{4})}=-0.125$

здесь не указано (предположил что x->0 - что дает повод обратиться к одной из замечательных границ)

$lim_{x->0} \frac{5sin(\frac{1}{2}x)}{2x}=\\ lim_{x->0} \frac{5sin(\frac{1}{2}x)}{4*(\frac{1}{2}x)}=\frac{5*1}{4}=1.25$

$lim_{x->0} \frac{\sqrt{1-x}-1}{x^2}=\\ lim_{x->0} \frac{(\sqrt{1-x}-1)(\sqrt{1-x}+1)}{x^2(\sqrt{1-x}+1)}=\\ lim_{x->0} \frac{1-x-1}{x^2(\sqrt{1-x}+1)}=\\ lim_{x->0} \frac{-x}{x^2(\sqrt{1-x}+1)}=\\ lim_{x->0} \frac{-1}{x(\sqrt{1-x}+1)}=-\infty$
- Автор:
  burch
- 6 лет назад
- 0
Добавить свой ответ