Задать вопрос Регистрация
Помочь другим

  • Народ! Буду благодарна объяснению как найти производную от

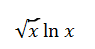
    question img

Ответы 2

  • Большое спасибо! Очень понятно и доступно объяснили, а то я сижу и думаю^^
  • Производная от умножения берется так:(uv)'=u'v+v'u   (1)Здесь u=\sqrt{x},  v=\ln x(\sqrt x)'=(x^{\frac{1}{2}})=\frac{1}{2}x^{\frac{1}{2}-1}==\frac{1}{2}x^{-\frac{1}{2}}=\frac{1}{2x^{\frac{1}{2}}}==\frac{1}{2\sqrt{x}}Значит u'=(\sqrt{x})'=\frac{1}{2\sqrt{x}}С другой стороны(\ln x)'=\frac{1}{x}По формуле (1) получаем(\sqrt{x}\ln x)'=\frac{\ln{x}}{2\sqrt{x}}+\frac{\sqrt{x}}{x}==\frac{\ln{x}}{2\sqrt{x}}+\frac{1}{\sqrt{x}}=\frac{\ln{x}+2}{2\sqrt{x}}Ответ: (\sqrt{x}\ln x)'=\frac{\ln{x}+2}{2\sqrt{x}}

    • Автор:

      travis87
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years