Задать вопрос Регистрация
Помочь другим

  • Как выудить значение функции из этого решения? Символьное решение (Mathcad prime)

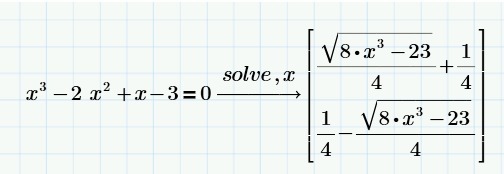
    question img

Ответы 3

  • А у Вас решение не законченное и может быть, даже не верное

    • Автор:

      turtle
    • 6 лет назад
    • 0
  • Оно верное.Это метод Виетта -Кардано. а сомневаться - это вполне нормальный процесс. Если Вам интересно приблизительное значение корней , то х1,2≈ -0,00873±1,1713i x3≈2,1746
  • Ваш Маткад как-то странно решаетВот что получилось у меня( с учётом иррациональных корней)x_{1} = - \frac{1}{2} \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}} - \frac{1}{18 \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}} + \frac{2}{3} + i \left(- \frac{\sqrt{3}}{2} \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}} + \frac{\sqrt{3}}{18 \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}}ight) \\ x_{2} = - \frac{1}{2} \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}} - \frac{1}{18 \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}} + \frac{2}{3} + i \left(- \frac{\sqrt{3}}{18 \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}} + \frac{\sqrt{3}}{2} \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}ight) \\ x_{3} = \frac{1}{9 \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}} + \frac{2}{3} + \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}

    • Автор:

      enrique
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years