-
Задача 16
К питающей сети с напряжением 110B параллельно подключены
конденсатор и катушка индуктивности с активным сопротивлением
5 Ом и индуктивностью 0,02 Гн. При частоте питающего
напряжения 120 ГцВ контуре возник резонанс. Определить емкость
конденсатора и ток в неразветвленной части цепи при резонансе.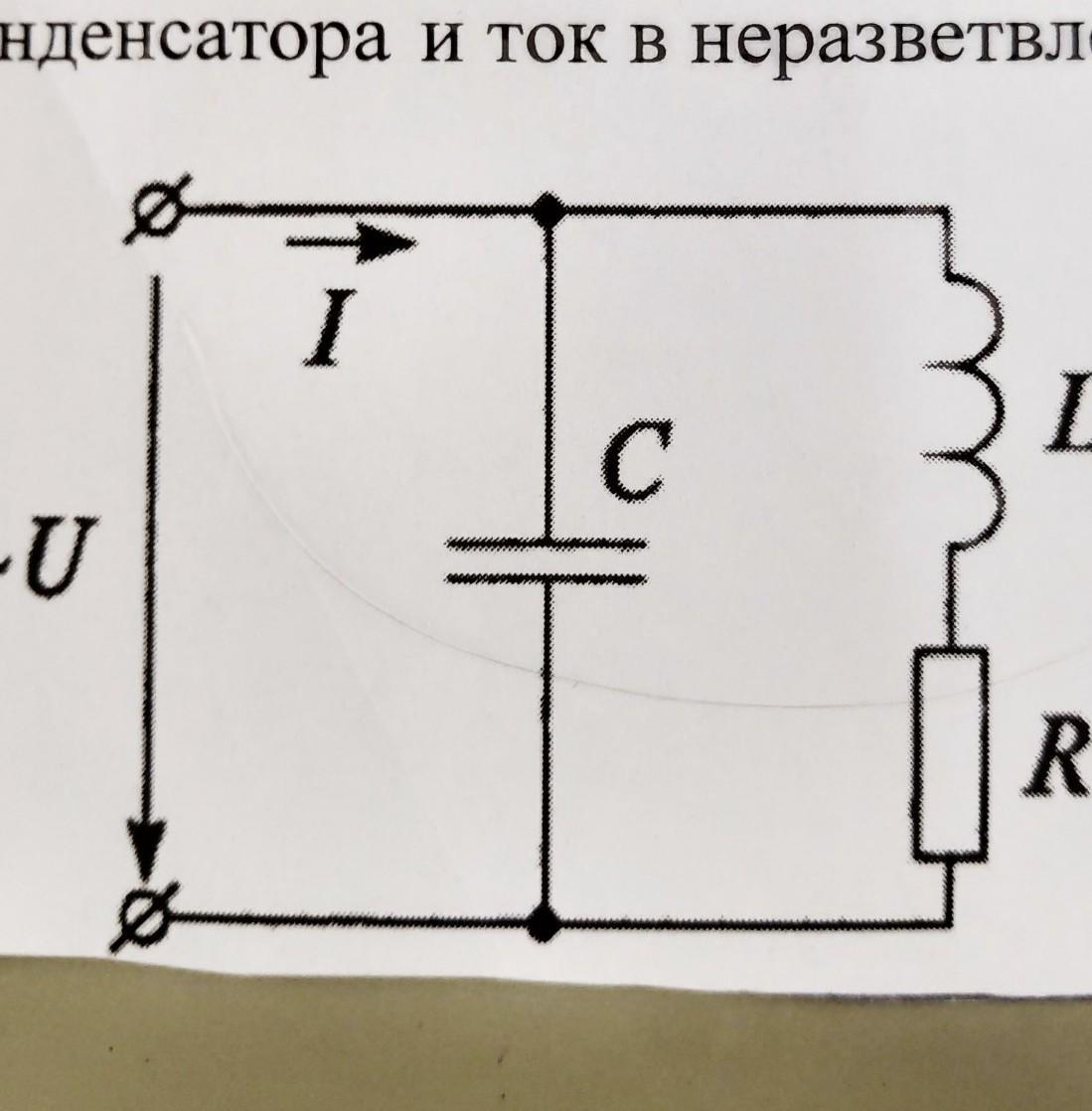
-
Предмет:
Другие предметы -
Автор:
thumper100 - 6 лет назад
-
Ответы 1
-
Перед расчетом емкости конденсатора и тока в неразветвленной части цепи при резонансе необходимо найти резонансную частоту контура, используя формулу:
ω₀ = 1 / sqrt(LC),
где L - индуктивность катушки, С - емкость конденсатора.
Подставляем известные значения:
ω₀ = 1 / sqrt(0,02 C)
Частота питающего напряжения равна 120 Гц, то есть угловая частота ω = 2πf равна 2π120 рад/с.
При резонансе ω₀ = ω, следовательно:
1 / sqrt(0,02 C) = 2π120
C = 1 / (4π² 0,02 (120)²) ≈ 1,77 мкФ
Теперь, когда мы нашли емкость конденсатора, можем найти ток в неразветвленной части цепи при резонансе, используя формулу:
I = U / R,
где U - напряжение на конденсаторе или катушке при резонансе, R - активное сопротивление цепи.
Поскольку контур находится в резонансе, напряжение на катушке и конденсаторе равно напряжению питающей сети, т.е. U = 110 В.
Активное сопротивление цепи равно сумме активного сопротивления катушки и реактивного сопротивления конденсатора. При резонансе реактивное сопротивление конденсатора равно реактивному сопротивлению катушки и противоположно ему по знаку, поэтому они компенсируют друг друга и результирующее сопротивление цепи равно активному сопротивлению катушки, т.е. R = 5 Ом.
Подставляем известные значения:
I = 110 / 5 ≈ 22 А
Таким образом, емкость конденсатора равна 1,77 мкФ, а ток в неразветвленной части цепи при резонансе равен 22 А.
-
Автор:
Fedoseewa27 - 2 года назад
-
0
-
-
Добавить свой ответ
-
в наклонной треугольной призме расстояние между боковыми ребрами равны 10;10;12см, а боковое ребро равно15. Выписать площадь боковой поверхности призмы
-
Предмет:
Математика -
Автор:
cailynbarr - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Функція y=kx, її властивості і графік
-
определить число оборотов электродвигателя постоянного тока при напряжении 220в, если ток якоря 113а сопротивление 1,635ом , а магнитный поток полюсов равен 0,001вб. Постоянная машины С равна 36
-
Предмет:
Другие предметы -
Автор:
ramirosharp - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Вычислить производную сложной функции y=ln2x-1
-
Предмет:
Математика -
Автор:
jake17 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
