-
Якщо сторону квадрата збільшити на 20 %, тоді його площа збільшиться на 99дм2. Обчисли сторону квадрата і його площу до збільшення.
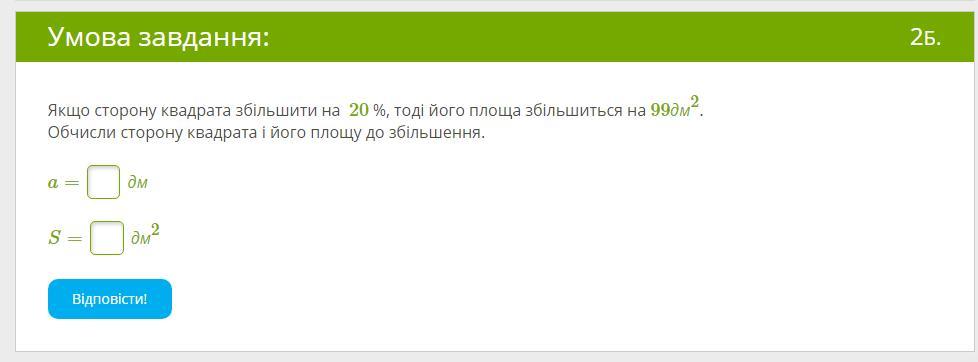
-
Предмет:
Другие предметы -
Автор:
morganmullins - 2 года назад
-
Ответы 1
-
Ответ:
Нехай x - довжина сторони квадрата до збільшення.
Згідно умови, якщо сторону квадрата збільшити на 20%, то вона становитиме 1.2x (120% від x).
Далі, знайдемо площу квадрата до збільшення:
площа = x^2
Знайдемо площу квадрата після збільшення:
площа + 99 = (1.2x)^2 = 1.44x^2
Запишемо рівняння за умовою:
1.44x^2 = x^2 + 99
Розв'яжемо його:
0.44x^2 = 99
x^2 = 99 / 0.44
x^2 ≈ 225
x ≈ 15
Отже, сторона квадрата до збільшення становила 15 дм, а його площа дорівнювала 225 дм^2.
Після збільшення, сторона квадрата становитиме 1.2 * 15 = 18 дм, а його площа буде дорівнювати 1.44 * 225 = 324 дм^2.
-
Автор:
sadie15nc - 2 года назад
-
1
-
-
Добавить свой ответ
Еще вопросы
- найти значение работы Если пружина с коэффициентом жёсткости 350 НМ растянулась 3 см до 10 смпомогите дам 20 баллов
-
Випишіть із Мауглі слова (по 3 - 5 ), що характеризують світ джунглів, і класифікуйте їх за групами: "Тварини", "Птахи" , "Рослини" , "Природні явища" . Допоможітььь. Саме характеристику.
-
Предмет:
Литература -
Автор:
kaitlynnsummers - 2 года назад
-
Ответов:
1 -
Смотреть
-
- найти силу тяги при движении тела на 5 км если скорость тела изменён с 300 км/ч в 100 км/ч масса тела 2 тпжж помогите20б
- Що входило у реформи Ататюрка? А) ліквідація іноземних концесій; Б) легалізація профспілок; В) багатопартійна система; Г) законодавство за європейським зразком; Д) надання прав жінкам.
How much to ban the user?
1 hour
1 day
100 years
