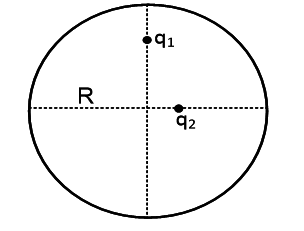
Определить поток вектора напряженности электростатического поля через поверхность сферы радиусом 10 см, внутри которой находятся два точечных заряда q1=-2нКл и q2=+5нКл (см. рисунок).

может поможет

§5 Поток вектора напряженности   Определим поток вектора  через произвольную поверхность dS,   - нормаль к поверхности.α - угол между нормалью и силовой линией вектора . Можно ввести   вектор площади . ПОТОКОМ ВЕКТОРА  называется скалярная величина ФЕ равная скалярному произведению вектора напряженности  на вектор площади   Для однородного поля   Для неоднородного поля где - проекция  на ,  - проекция  на . В случае криволинейной поверхности S ее нужно разбить на элементарные поверхности dS, рассчитать поток  через элементарную поверхность, а общий поток будет равен сумме или в пределе интегралу от элементарных потоков где  - интеграл по замкнутой поверхности S (например, по сфере, цилиндру, кубу и т.д.) Поток вектора   является алгебраической величиной: зависит не только от конфигурации поля , но и от выбора направления . Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т.е. нормаль, направленная наружу области, охватываемой поверхностью.                     Для однородного поля поток через замкнутую поверхность равен нуля. В случае неоднородного поля   .   §6 Теорема Гаусса и ее применение к расчету напряженности электростатического поля   I. Рассмотрим электростатическое поле, создаваемое единичным положительным зарядом. Заключим его в сферу радиуса R. Определим поток напряженности  через сферическую поверхность радиуса R. Разобъем поверхность S сферы на элементарные площадки dS. Нормаль к площадке dS направлена по линии радиуса сфера и совпадает с направлением вектора :  параллельна  поэтому                   Тогда поток вектора  через поверхность S будет равен сумме потоков через элементарные площадки dS и устремляя dS к 0 можно записать, что Учитывая, что напряженность поля точечного заряда равна получим         Этот результат можно обобщить на случай любой поверхности. Учитывая принцип суперпозиции можно полученный результат применить к любому количеству зарядов, находящихся внутри поверхности. ТЕОРЕМА ГАУССА: Поток вектора напряженности через произвольную замкнутую поверх­ность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ε0 (ε0 - электрическая постоянная)   II. Применение теоремы Гаусса. Напряженность поля, создаваемая бесконечно протяженной однородно заряженной плоскоти с поверхностной плотностью заряда σ.ПОВЕРХНОСТНАЯ ПЛОТНОСТЬ ЗАРЯДА показывает, какой заряд приходится на единицу площади Пинии напряженности  перпендикулярны рассматриваемой поверхности и направлены от нее в обе стороны. Построим цилиндр с основанием S, образующая которого параллельна линиям напряженности .     Так как образующая цилиндра параллельна  , то поток через основание S равен Поток через боковую поверхность цилиндра равен нулю, т.к.  перпендикулярна S cosα= cos90° = 0, следовательно, 2. Напряженность поля, создаваемая двумя параллельными бесконечно протяженными пластинами с поверхностной плотностью зарядов +σ и -σ. Найден поле Е, используя принцип суперпозиции полей. В области между плоскостями Слева и справа от плоскостей поля вычитаются, т.к. линии напряженности направлены навстречу друг другу  .   3. Напряженность ноля, создаваемая бесконечно протяжённой  нитью с линейной плотностью заряда τ. Линейная плотность заряда            показывает,   какой заряд приходится на единицу длина проводника. Требуется определить напряженность ноля на некотором расстоянии r от нити. Для этого построим цилиндр радиуса r и высотой h, по оси которого проходит нить. Поток через основания рассматриваемого цилиндра равен нулю, т.к.  перпенди­кулярна вектору , следовательно, поток будет определяться только потоком через боковую поверхность цилиндра 4. Напряженность поля, создаваемого сферической поверхностью с поверхностной плотностью заряда σ. На сфере радиуса R распределен заряд q. Поверхностная плотность заряда   Линии напряженности направлены радиально, отходя от поверхности сфера под прямым углом. Окружаем данную сферу сферой радиуса r и определяем поток напряженности  через cферическую поверхность радиуса r.               При r > R весь заряд q попадает внутрь сфера r. Тогда по теореме Гаусса   , т.к. Еn = E.                                 При r < R внутри поверхности радиуса r зарядов нет и поэтому Е=0. На этом основано экранирование - защита от внешних электрических полей.   5. Напряженность поля объемно заряженного шара с объемной плотностью заряда ρ. Объемная плотность заряда показывает, какой заряд приходится на единицу объема а) При r > R по пункту 4 находим                        б) При r < R