Деревянный и алюминиевый цилиндры одинакового сечения соединены в торец. Длина деревянного цилиндра 20 см. Какую длину должен иметь алюминиевый цилиндр, чтобы при плавании в воде цилиндры устанавливались вертикально, причем верхнее основание деревянного цилиндра находилось бы на 2,9 см выше уровня воды? (рд = 800 кг/м3.)

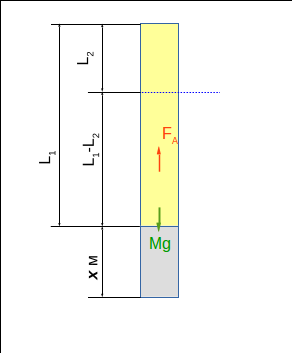
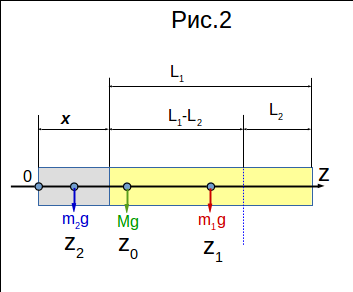
ДаноL₁=20 см =0,2 м длина деревянного цилиндра;L₂=2,9 см=0,029 см длина выступающей над водой части деревянного цилиндра;ρ₁=800 кг/м³  плотность дереваρ₂=2700 кг/м³  плотность алюминияρ=1000 кг/м³ плотность воды Сообразим рисунок (рисунок 1).Итак чтобы составной цилиндр при плавал, необходимо, чтобы сила тяжести Mg уравновешивалась силой Архимеда F_A. Обозначим площадь поперечного сечения S. Тогда в положении требуемого равновесия сила Архимеда. F_A=\rho gV_3=\rho gS(L_1-L_2+x) (1)где V₃ - Объем погруженной части составного цилиндра.Сила тяжестиF_t=Mg=(\rho_1V_1+\rho_2V_2)g=(\rho_1SL_1+\rho_2Sx))g=(\rho_1L_1+\rho_2x))Sg  (2)Приравниваем правые части (1) и (2) и разрешаем полученное уравнение относительно x.\rho gS(L_1-L_2+x)=gS(\rho_1L_1+\rho_2x) \newline \newline \rho (L_1-L_2+x)=\rho_1L_1+\rho_2x \newline \newline \rho( L_1-L_2)+\rho x=\rho_1L_1+\rho_2x \newline \newline \rho_2x-\rho x =\rho( L_1-L_2)-\rho_1L_1 \newline \newline x(\rho_2-\rho) =\rho( L_1-L_2)-\rho_1L_1 x =(\rho( L_1-L_2)-\rho_1L_1)/(\rho_2-\rho) (3)Подставляем числа в (3)x =(\rho( L_1-L_2)-\rho_1L_1)/(\rho_2-\rho)=\newline = (1000(0,2-0,029)-800 \cdot 0,2)/(2700-1000)= \newline =(1000\cdot 0,171-160)/1700=(171-160)/1700=11/1700\approx0,00647 м.Т.е. приблизительно 6,5 мм  P.S.Еще один момент. Для устойчивого вертикального плавания должно выполняться условие: центр плавучести (центр масс вытесненного объема воды должен быть выше, чем центр масс составного цилиндра) . Проверяем. У нас центр плавучести находится на уровне(L₁-L₂+x)/2=(0,171+0,0647)/2≈0,0887м от уровня воды. И на таком же расстоянии от нижнего торцаh≈0,0887м=8,87 см.  Положение центра масс составного цилиндра по быстрому определим так:Рассмотрим составной цилиндр в горизонтальном положении (рисунок 2)."Стянем" в точки своих центров масс z₁, z₂ деревянную и алюминиевую части, а затем найдем точку z₀ относительно которой моменты сил F1=m₁g и F2=m₂g , будут равны.Положение центра масс Z₁=x+L₁/2, соответственно Z₂=x/2Тогда моменты относительно точки Z₀M_1=m_1g(z_1-z_0)=\rho_1SL_1g(z_1-z_0) =\rho_1SL_1g(x+L_1/2-z_0) \newline M_2=m_2g(z_0-z_2)=\rho_2Sxg(z_0-z_2)=\rho_2Sxg(z_0-x/2) \newline \newline M_1=M_2 \newline \rho_1SL_1g(x+L_1/2-z_0) =\rho_2Sxg(z_0-x/2) \newline \rho_1L_1(x+L_1/2-z_0) =\rho_2x(z_0-x/2) \newline \rho_1L_1(x+L_1/2)-\rho_1L_1z_0 =\rho_2xz_0-\rho_2x^2/2 \newline \newline \rho_1L_1(x+L_1/2)+\rho_2x^2/2=\rho_2xz_0+\rho_1L_1z_0=z_0(\rho_2x+\rho_1L_1) \newlinez_0= \frac{\rho_1L_1(x+L_1/2)+\rho_2x^2/2}{(\rho_2x+\rho_1L_1)} z_0= \frac{\rho_1L_1(x+L_1/2)+\rho_2x^2/2}{(\rho_2x+\rho_1L_1)}= \frac{800\cdot 0,2(0,00647+0,1)+2700(11/1700)^2/2}{(2700\cdot11/1700+800\cdot0,2)}=\newline = \frac{160(0,10647)+1350(121/1700 \cdot 1700)}{(27\cdot11/17+160)}\approx0,0963 z₀≈0,0963м=9,63 смот нижнего торца. Таким образом центр масс  составного цилиндра оказался выше чем центр  плавучести (z₀>h), а значит вертикальное положение будет неустойчивым. И, пожалуй, при заданной высоте выступающей части строго вертикального плавания не получится