Уравнение движения груза x=x(t) (x- в см, t - в секундах) 5+40t^2. Радиус (в см) R2=30,r2=20;R1=50,r1=35.Пользуясь иллюстрацией за данным уравнением прямолинейного движения груза определите скорость и ускорение точки М механизма в момент времени, когда груз пройдёт путь S=0,34м.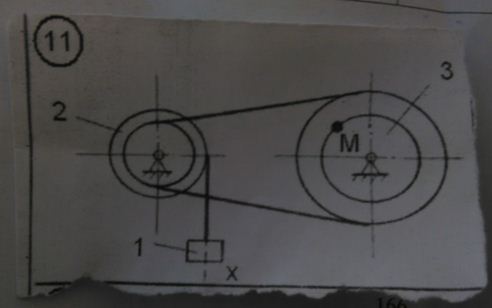

Уравнение движения груза x=x(t) (x- в см, t - в секундах) 5+40t^2.
Радиус (в см) R2=30,r2=20;R1=50,r1=35.Пользуясь иллюстрацией за данным уравнением прямолинейного движения груза определите скорость и ускорение точки М механизма в момент времени, когда груз пройдёт путь S=0,34м.
- Предмет:
  Физика
- Автор:
  ivángpww
- 5 лет назад

Ответы 5

Премного благодарен.
- Автор:
  vega
- 5 лет назад
- 0
Это ВУЗ или физмат-школа?
- Автор:
  ananíasrhtg
- 5 лет назад
- 0
Физмат-школа
- Автор:
  ripley
- 5 лет назад
- 0
Ясно. Нудноватая задача для школы. Но нужно учиться. Забыла сказать, если это важно: Верктор ускорения точки M будет направлен нестрого вниз между радиусом и касательной к точке M. Не строго вниз – означает вниз, но не строго вертикально.
- Автор:
  kyler
- 5 лет назад
- 0
$x(t) = 5 [ {_{CM}} ] + 40 [ \frac{_{CM}}{c^2} ] t^2$ ; $l_{r2} (t) = \frac{r_2}{R_2} x(t)$ – уравнение движения произвольной точки малого обода левого колеса вдоль самого обода. $l_{R1} (t) = l_{r2} (t) = \frac{r_2}{R_2} x(t)$ – уравнение движения произвольной точки большого обода правого колеса вдоль самого обода. $l_{r1} (t) = \frac{r_1}{R_1} l_{R1} (t) = \frac{r_1}{R_1} \frac{r_2}{R_2} x(t) = \frac{ r_1 r_2 }{ R_1 R_2} x(t)$ – уравнение движения произвольной точки малого обода правого колеса вдоль самого обода, т.е. это и есть уравнение движения точки M в полярной системе, вдоль окружности обода. Итак: $l_M (t) = \frac{ r_1 r_2 }{ R_1 R_2} x(t)$ ; $l_M (t) = \frac{ r_1 r_2 }{ R_1 R_2} ( 5 [ {_{CM}} ] + 40 [ \frac{_{CM}}{c^2} ] t^2 )$ ;Продифференцировав это выражение, мы и найдём скорость и тангенциальное ускорение: $v_M (t) = l'_M (t) = \frac{ r_1 r_2 }{ R_1 R_2} ( 80 [ \frac{_{CM}}{c^2} ] t )$ ; (I) $a_\tau (t) = l''_M (t) = 80 [ \frac{_{CM}}{c^2} ] \frac{ r_1 r_2 }{ R_1 R_2}$ ;Нормальное ускорение можно найти из кинематики вращения: $a_n (t) = \frac{ v_M^2 (t) }{ r_1 } = ( \frac{ 80 [ \frac{_{CM}}{c^2} ] r_2 t }{ R_1 R_2} )^2 r_1 = 80 [ \frac{_{CM}}{c^2} ] \frac{ r_1 r_2 }{ R_1 R_2} \frac{ 80 [ \frac{_{CM}}{c^2} ] t^2 r_2 }{ R_1 R_2 }$ ; $a_n (t) = \frac{ 80 [ \frac{_{CM}}{c^2} ] t^2 r_2 }{ R_1 R_2 } a_\tau (t)$ ; $\frac{ a_n (t) }{ a_\tau (t) } = \frac{ 80 [ \frac{_{CM}}{c^2} ] t^2 r_2 }{ R_1 R_2 }$ ; $a_M (t) = \sqrt{ a_\tau^2 + a_n^2 } = a_\tau \sqrt{ 1 + ( \frac{ a_n }{ a_\tau } )^2 } = 80 [ \frac{_{CM}}{c^2} ] \frac{ r_1 r_2 }{ R_1 R_2} \sqrt{ 1 + ( \frac{ 80 [ \frac{_{CM}}{c^2} ] t^2 r_2 }{ R_1 R_2 } )^2 }$ ; (II) $S = 5 [ {_{CM}} ] + 40 [ \frac{_{CM}}{c^2} ] t^2$ ;Из условия для времени движения, найдём t : $t^2 = \frac{ S - 5 [ {_{CM}} ] }{ 40 [ \frac{_{CM}}{c^2} ] } = \frac{ S / [ {_{CM}} ] - 5 }{ 40 } [c^2]$ ; $t = \frac{ [c] }{2} \sqrt{ \frac{ S / [ {_{CM}} ] - 5 }{ 10 } }$ ;Подставим это в выражения скорости (I) и ускорения (II): $v_M (t) = \frac{ r_1 r_2 }{ R_1 R_2} ( 4 [ \frac{_{CM}}{c} ] \sqrt{ 10 ( S / [ {_{CM}} ] - 5 ) } )$ ; (I*) $a_M (t) = 80 [ \frac{_{CM}}{c^2} ] \frac{ r_1 r_2 }{ R_1 R_2} \sqrt{ 1 + ( \frac{ ( 2S - 10 [ {_{CM}} ] ) r_2 }{ R_1 R_2 } )^2 }$ ; (II*)Вот и всё. Остался только арифметический расчёт.В результате скорость в см/с должна получиться близкой к числу, равному пятой степени двойки, а ускорение, выраженное в см/с^2 должно получиться числом, совпадающим со вторым годом после окончания II-ой Мировой Войны.||||| ВТОРОЙ СПОСОБ (более техничный) |||||Обозначим: $x_o = 5 [ {_{CM}} ]$ и $a = 80 [ \frac{_{CM}}{c^2} ]$ ;теперь нигде можно не учитывать размерности, они автоматически учтутся во введённых константах: $x(t) = x_o + \frac{ a t^2 }{2}$ ; $l_{r2} (t) = \frac{r_2}{R_2} x(t)$ – уравнение движения произвольной точки малого обода левого колеса вдоль самого обода. $l_{R1} (t) = l_{r2} (t) = \frac{r_2}{R_2} x(t)$ – уравнение движения произвольной точки большого обода правого колеса вдоль самого обода. $l_{r1} (t) = \frac{r_1}{R_1} l_{R1} (t) = \frac{r_1}{R_1} \frac{r_2}{R_2} x(t) = \frac{ r_1 r_2 }{ R_1 R_2} x(t)$ – уравнение движения произвольной точки малого обода правого колеса вдоль самого обода, т.е. это и есть уравнение движения точки M в полярной системе, вдоль окружности обода. Итак: $l_M (t) = \frac{ r_1 r_2 }{ R_1 R_2} x(t)$ ; $l_M (t) = \frac{ r_1 r_2 }{ R_1 R_2} ( x_o + \frac{ a t^2 }{2} )$ ;Продифференцировав это выражение, мы и найдём скорость и тангенциальное ускорение: $v_M (t) = l'_M (t) = \frac{ r_1 r_2 }{ R_1 R_2} a t$ ; (I) $a_\tau (t) = l''_M (t) = \frac{ r_1 r_2 }{ R_1 R_2 } a$ ;Нормальное ускорение можно найти из кинематики вращения: $a_n (t) = \frac{ v_M^2 (t) }{ r_1 } = ( \frac{ a r_2 t }{ R_1 R_2} )^2 r_1 = ( \frac{ a t^2 r_2 }{ R_1 R_2 } ) \frac{ r_1 r_2 }{ R_1 R_2} a$ ; $a_n (t) = \frac{ a t^2 r_2 }{ R_1 R_2 } a_\tau (t)$ ; $\frac{ a_n (t) }{ a_\tau (t) } = \frac{ a t^2 r_2 }{ R_1 R_2 }$ ; $a_M (t) = \sqrt{ a_\tau^2 + a_n^2 } = a_\tau \sqrt{ 1 + ( \frac{ a_n }{ a_\tau } )^2 } = a \frac{ r_1 r_2 }{ R_1 R_2} \sqrt{ 1 + ( \frac{ a t^2 r_2 }{ R_1 R_2 } )^2 }$ ; (II) $S = x_o + \frac{ a t^2 }{2}$ ;Из условия для времени движения, найдём t : $a t^2 = 2 ( S - x_o )$ ; $t = \sqrt{ 2 \frac{ S - x_o }{a} }$ ;Подставим это в выражения скорости (I) и ускорения (II): $v_M (t) = \frac{ r_1 r_2 }{ R_1 R_2} ( \sqrt{ 2 a ( S - x_o ) } )$ ; (I*) $a_M (t) = a \frac{ r_1 r_2 }{ R_1 R_2} \sqrt{ 1 + ( \frac{ 2 ( S - x_o ) r_2 }{ R_1 R_2 } )^2 }$ ; (II*)Арифметический расчёт и в этом случае, разумеется, даст те же результаты. Но сами формулы, не содержащие единиц измерения, выглядят более компактно.
- Автор:
  ignacio83
- 5 лет назад
- 0
Добавить свой ответ