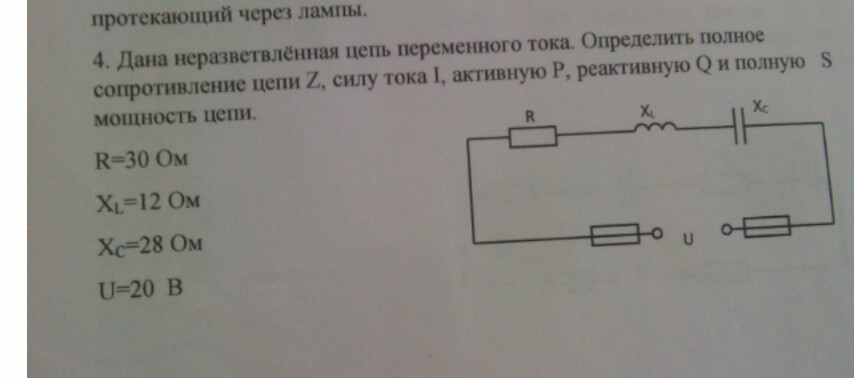
Определить полное сопротивление, силу тока, активную, реактивную и полную мощности

Определить полное сопротивление, силу тока, активную, реактивную и полную мощности
- Предмет:
  Физика
- Автор:
  franciscohart
- 5 лет назад

Ответы 6

Ок. Но там же не чат...
- Автор:
  annie96
- 5 лет назад
- 0
Я научу Вас делать чат, если это Вас интересует)
- Автор:
  cocosoto
- 5 лет назад
- 0
А тут тем более не чат. Каждое сообщение потом модераторы удаляют руками.
- Автор:
  morganbprl
- 5 лет назад
- 0
Может быть. Если у меня время потом ещё будет... Хорошо.
- Автор:
  jaggervfle
- 5 лет назад
- 0
Всех – с Новым Годом. Bye!
- Автор:
  blake49
- 5 лет назад
- 0
Полная мощность $S$ может быть вычислена, как: $S = U_e^2/|z| ,$ где $U_e$ – эквивалентное напряжение (не амплитудное) сети переменного тока, а $z$ – полный импеданс цепи. Полная мощность, эта та самая мощность, которая регулярно нагружает источник переменного напряжения, но поскольку в ёмкостно-индуктивной цепи существует сдвиг фаз между током и напряжением, в силу чего часть мощности регулярно возвращается обратно в источник переменного напряжения – активная (потребляемая) мощность $P$ оказывается меньше полной.Активная (потребляемая) мощность $P$ может быть вычислена, как: $P = U_e^2 \cdot \frac{R}{z^2} ,$ где $R$ – полное активное (омическое) сопротивление цепи.Реактивная мощность $Q$ может быть вычислена, как: $Q^2 = S^2 - P^2$ ;Учитывая данные задачи, найдём, что: $z^2 = R^2 + ( X_L - X_C )^2 ,$ тогда: $Q^2 = S^2 - P^2 = \frac{U_e^4}{z^2} ( 1 - \frac{ R^2 }{ z^2 } ) = \frac{U_e^4}{z^2} ( 1 - \frac{ R^2 }{ R^2 + ( X_L - X_C )^2 } ) =$ $= \frac{U_e^4}{z^2} \frac{ ( X_L - X_C )^2 }{ R^2 + ( X_L - X_C )^2 } = \frac{U_e^4}{z^4} ( X_L - X_C )^2$ ; $|Q| = \frac{U_e^2}{z^2} | X_L - X_C |$ ;Не сказано, является данное в задаче напряжение амплитудным или эффективным, но по-умолчанию обычно всегда указывается эффективное, учитывая это вычислим последовательно все величины : $z^2 = R^2 + ( X_L - X_C )^2 \approx ( 30^2 + ( 12 - 28 )^2 )$ Ом² $=$ $= ( 900 + 16^2 )$ Ом² $= 1156$ Ом² ; $|z| = \sqrt{z^2} \approx \sqrt{1156}$ Ом $= 34$ Ом .Полный ток в системе определяется, как: $I = U/|z| \approx 20/34 A \approx 0.588 A = 588$ мА . $S = U_e^2/|z| \approx 20^2/34$ Вар $\approx 11.8$ Вар – полная мощность $P = U_e^2 \frac{R}{z^2} \approx 20^2 \cdot \frac{30}{1156} \approx 10.4$ Вт – активная (потребляемая) мощность. $|Q| = \frac{U_e^2}{z^2} | X_L - X_C | \approx \frac{20^2}{1156} | 12 - 28 | \approx 5.54$ Вар – реактивная мощность.О т в е т : $|z| \approx 34$ Ом – полное сопротивление (модуль импеданса). $I \approx 588$ мА – эффективный ток в цепи. $S \approx 11.8$ Вар – полная мощность $P \approx 10.4$ Вт – активная (потребляемая) мощность. $|Q| \approx 5.54$ Вар – реактивная мощность.
- Автор:
  tex
- 5 лет назад
- 0
Добавить свой ответ