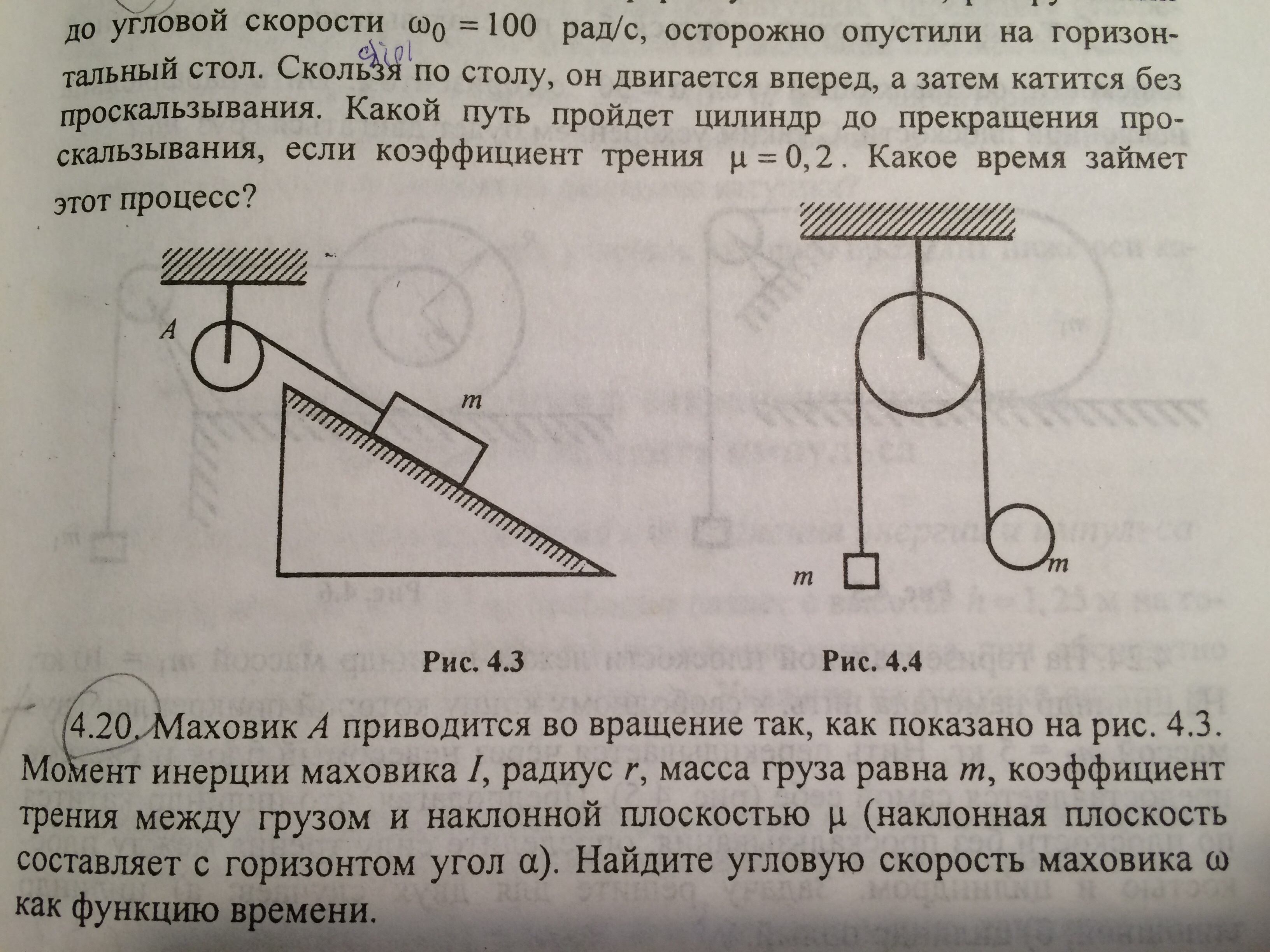
Маховик А приводиться во вращение так, как показано на рис. 4.3. Момент инерции маховика I, радиус r, масса груза равна m, коэффициент то между грузом и наклонной плоскостью u. Найдите угловое ускорение!

Вычисляешь момент инерции шкива по формуле момента инерции диска: J=m*r²=0,2*0,05²=5*10⁻⁵ кг*м² Вычисляешь момент инерции маховика по формуле момента инерции кольца: J=M*R²=1*0,4²=0,16 кг*м² Суммарный момент инерции всей системы равен J=0,16+5*10⁻⁵=0,16005 кг*м² Теперь записываешь второй закон Ньютона для опускающегося груза массой m=0,5 кг в проекции на вертикальную ось: m*a=m*g-T     ❶ T -- это сила натяжения нити. Основное уравнение динамики вращательного движения для системы "маховик+шкив" тоже надо записать: J*ε=M     ❷ Вращающий момент силы натяжения нити равен M=T*r     ❸ Еще надо записать формулу связи между угловым ускорением ε (вращается шкив+маховик) и ускорением груза массой m: a=ε*r     ❹ Откуда она взялась? А все оттуда, из дифференцирования по времени простенькой школьной формулы v=ω*r Подставляешь числа в формулы ❶, ❷, ❸, ❹, получаешь систему линейных уравнений с четырьмя неизвестными. Решаешь и находишь угловое ускорение ε. Теперь самое главное: вопросы внимательнее надо писать! Ни черта непонятно, чё в задаче надо найти-то... Во всяком случае, для вращающегося маховика справедлива формула для угловой скорости ω=ε*t.