Задать вопрос Регистрация
Помочь другим

  • Брусок массы m лежит на плоскости, наклоненной
    под углом α к горизонту. На него действует
    горизонтальная сила F (см. рисунок). Определите
    ускорение бруска. Коэффициент трения бруска о
    плоскость M.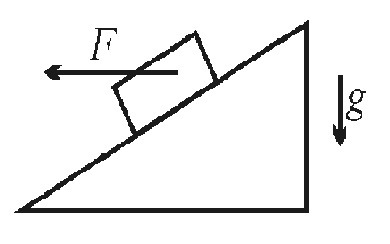

    question img

Ответы 2

  • Два случая, случай 2 дробится на две ситуации 2a и 2b и ситуация 2b дробится еще на два варианта 2b-1 и 2b-2
  • В задаче есть случаи, но надо сначала сказать что-нибудь точноСпроецируем все силы на ось, перпендикулярную плоскости, предполагая, что тело все-таки лежит на ней, а не отрывается от нее внешней силой F0 = mg\cos\alpha - N - F\sin\alpha\\ N = mg\cos\alpha - F\sin\alphaИтак, поскольку сила реакции опоры не может быть меньше нуля, находим первое ограничение на силу FF\sin\alpha\leq mg\cos\alpha\\ F \leq mg\cot\alphaПоработаем в этом режиме. Сила F и сила тяжести стремятся двигать брусок вниз вдоль плоскости, значит сила трения направлена вверх вдоль плоскости. Тут также возможны два случая - тело покоится и тело стоит. Найдем в каком случае тело будет покоиться.0 = F\cos\alpha+mg\sin\alpha-F_t\\ F_t = F\cos\alpha+mg\sin\alphaСила трения не может превышать μN, поэтому\mu(mg\cos\alpha - F\sin\alpha)\geq F\cos\alpha+mg\sin\alpha\\ F(\cos\alpha+\mu\sin\alpha)\leq mg(\mu\cos\alpha-\sin\alpha)\\ F \leq mg\frac{\mu\cos\alpha-\sin\alpha}{\mu\sin\alpha + \cos\alpha}Отметим, что при μ<tgα неравенство теряет смысл, и брусок не сможет ни при каких F, покоиться на плоскости, в ином случае это будет возможно при некоторых малых значениях силы F, и ускорение будет 0. Если брусок движется, тоma = F\cos\alpha+mg\sin\alpha - \mu N = \\F\cos\alpha+mg\sin\alpha -\mu(mg\cos\alpha - F\sin\alpha) = \\ F(\cos\alpha+\mu\sin\alpha) + mg(\sin\alpha-\mu\cos\alpha)\\ a = \frac{F}{m}(\cos\alpha+\mu\sin\alpha) +g(\sin\alpha-\mu\cos\alpha)Наконец вернемся к случаю, когда сила отрывает брусок от клина. Тогда у тела будет горизонтальное ускорение F/m и вертикальное g, поэтому полное ускорение составитa = \sqrt{(F/m)^2+g^2}Соберем ответ1) F \ \textgreater \ mg\cot\alphaa = \sqrt{(F/m)^2+g^2}2)F\ \textless \ mg\cot\alpha2a)μ<tgαa = \frac{F}{m}(\cos\alpha+\mu\sin\alpha) +g(\sin\alpha-\mu\cos\alpha)2b)μ >= tgα2b-1)F \leq mg\frac{\mu\cos\alpha-\sin\alpha}{\mu\sin\alpha + \cos\alpha}a = 02b-2)F\ \textgreater \ mg\frac{\mu\cos\alpha-\sin\alpha}{\mu\sin\alpha + \cos\alpha}такой же ответ как и в 2а

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years