-
Опредетите сопротивление R(ab) между точкамм A и B проволочной сетки, показанной на рисунке. Сопротивление каждого из проводников(вне зависимости от его длины), из которых спаяна сетка = R. Места спайки проводников обозначены точками. В центре сетки электрический контакт отсутствует.
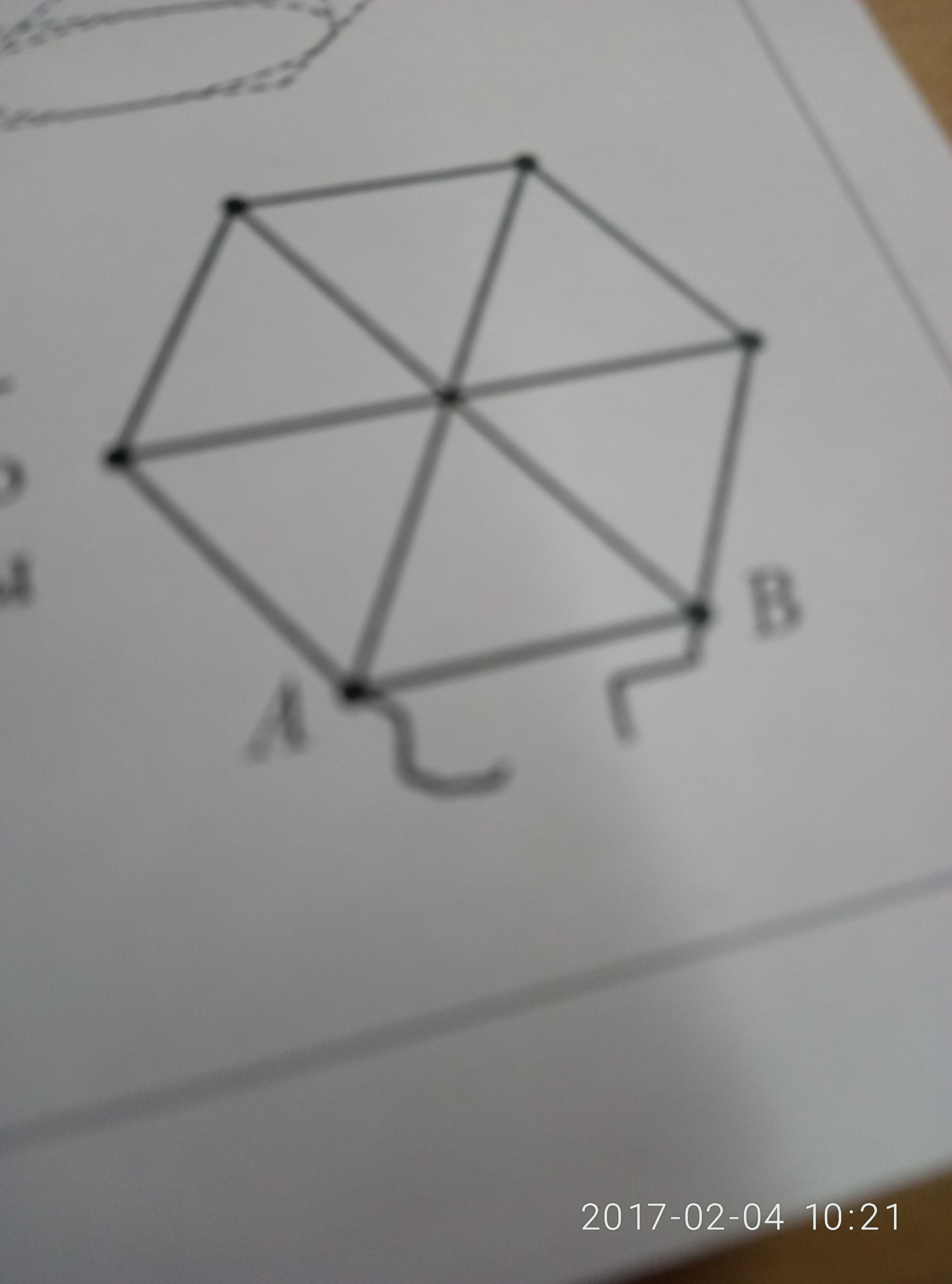
-
Предмет:
Физика -
Автор:
killianfitzpatrick - 5 лет назад
-
Ответы 1
-
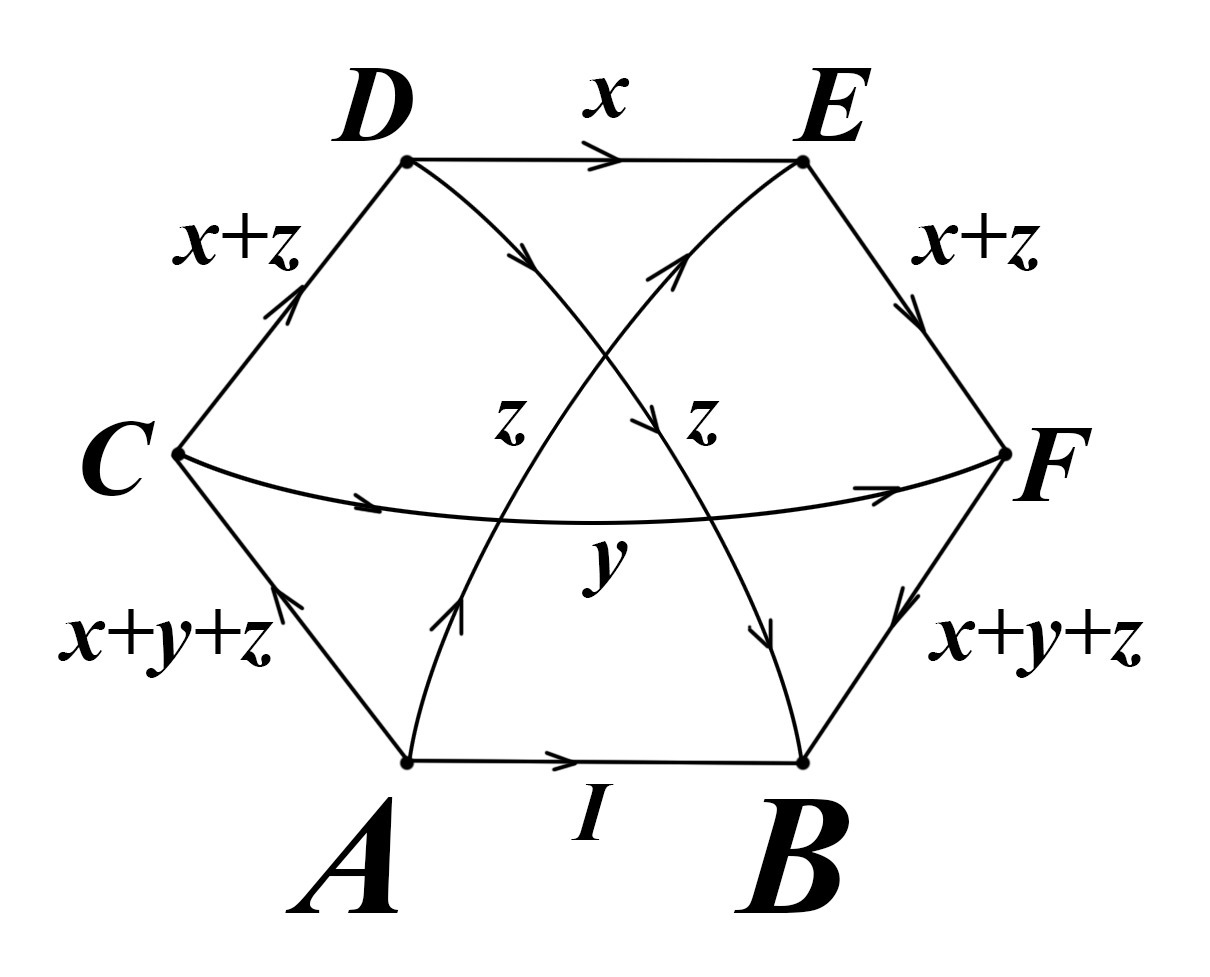
Смотрите иллюстрацию к решению задачи.Обозначим ток через нижний проводник, как: I \ . Обозначим ток между точками D и E, как: x \ , ток между точками C и F, как: y \ , а ток между точками А(B) и E(D), как: z \ . Равенство последних токов следует из симметрии.Из точки D вытекают токи x и z \ , а значит и втекает ток x+z \ . Из точки C вытекают токи x+z и y \ , а значит и втекает ток x+y+z \ . Для разности потенциалов между точками A и B можно записать уравнение: (x+y+z)R + yR + (x+y+z)R = IR \ ; Для разности потенциалов между точками C и F можно записать уравнение: (x+z)R + xR + (x+z)R = yR \ ; Для разности потенциалов между точками A и E можно записать уравнение: (x+y+z)R + (x+z)R + xR = zR \ ; Получаем три уравнения: 2x + 3y + 2z = I \ ; 3x + 2z - y = 0 \ ; 3x + y + z = 0 \ ; Вычтем из первого второе: 4y - x = I \ ; Вычтем из удвоенного последнего второе: 3x + 3y = 0 \ ; Итак: x =- y \ ; 5y = I \ ; y = \frac{I}{5} \ ; x = - \frac{I}{5} \ ; z = \frac{2}{5}I \ ; А значит, из точки A в совокупности вытекает ток: I_A = I + z + x+y+z = \frac{9}{5} I \ , Так как будто бы между точками A и B подключено сопротивления в \frac{9}{5} раз меньшее, чем R \ , а это как раз и определяет эквивалентное сопротивление сетки: R_{AB} = R : \frac{9}{5} = \frac{5}{9} R \ ; ОТВЕТ: R_{AB} = \frac{5}{9} R \ .
-
Автор:
marcianordma - 2 года назад
-
19
-
-
Добавить свой ответ
Еще вопросы
-
ПОМОГИТЕ ПЖ СОСТАВИТЬ 5 ПРЕДЛОЖЕНИЯ ЛЕТУЧИЕ МЫШИ
-
Предмет:
Окружающий мир -
Автор:
madalynnhorn - 5 лет назад
-
Ответов:
3 -
Смотреть
-
-
образуй другие формы имени прилагательного птичий
-
Предмет:
Русский язык -
Автор:
amorcitajh2s - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
x^2+x^3=x^3+x^4
ПОМОГИТЕ РЕШИТЬ-
Предмет:
Алгебра -
Автор:
jovani0vmd - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Какой генотип у бабочек птиц и пресмыкающихся
-
Предмет:
Биология -
Автор:
marielacherry - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
