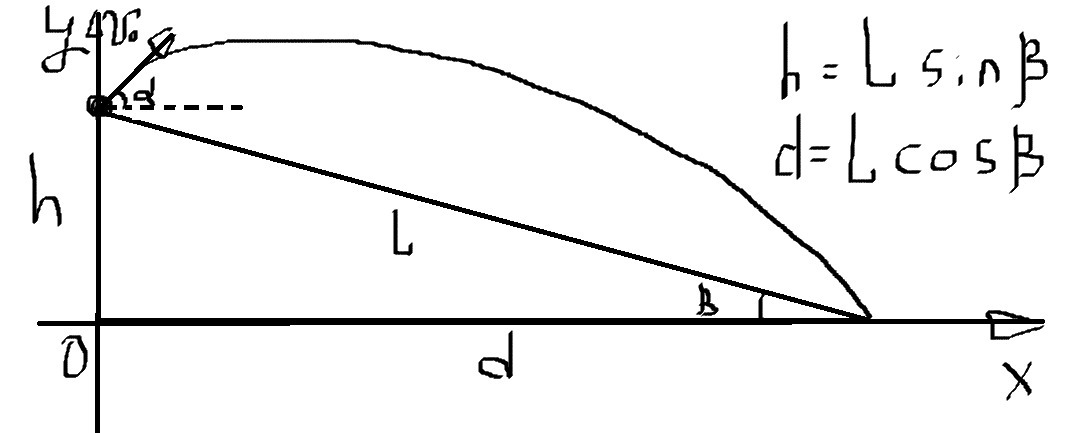
С вершины холма, склон которого составляет с горизонтом угол β=10град, брошен с начальной скоростью v0=15м/с камень вверх под углом α=15град к го- ризонту. Точка падения камня находится от вершины на расстоянии L (считая вдоль склона холма). Определите L - ?

Если можно с рисунком .

• идея решения: написать уравнения координат для осей X и Y, выразить перемещения вдоль них через прямоугольный треугольник и решить получившуюся систему уравнений○ L cosβ = v0 cosα t○ 0 = L sinβ + v0 sinα t - (g t²)/2• из первого уравнения t = (L cosβ)/(v0 cosα). подставляем его во второе:○ (g/2) * ((L cosβ)/(v0 cosα))² - v0 sinα * (L cosβ)/(v0 cosα) - L sinβ = 0○ L² * (g cos²β)/(2 v0² cos²α) - L (tgα cosβ + sinβ) = 0○ L ((g cos²β)/(2 v0² cos²α) L - (tgα cosβ + sinβ)) = 0○ L = (tgα cosβ + sinβ) * ((2 v0² cos²α)/(g cos²β))○ L = (0.2679*0.9848+0.1736) * ((2*225*0.933)/(9.8*0.9698)) ≈ 19.3 м