Тело брошенное вертикально вверх, возвратилось в точку бросания. Определить отношение времени спуска ко времени подъема, если масса тела равна 0,5кг, а сила сопротивления 3 H

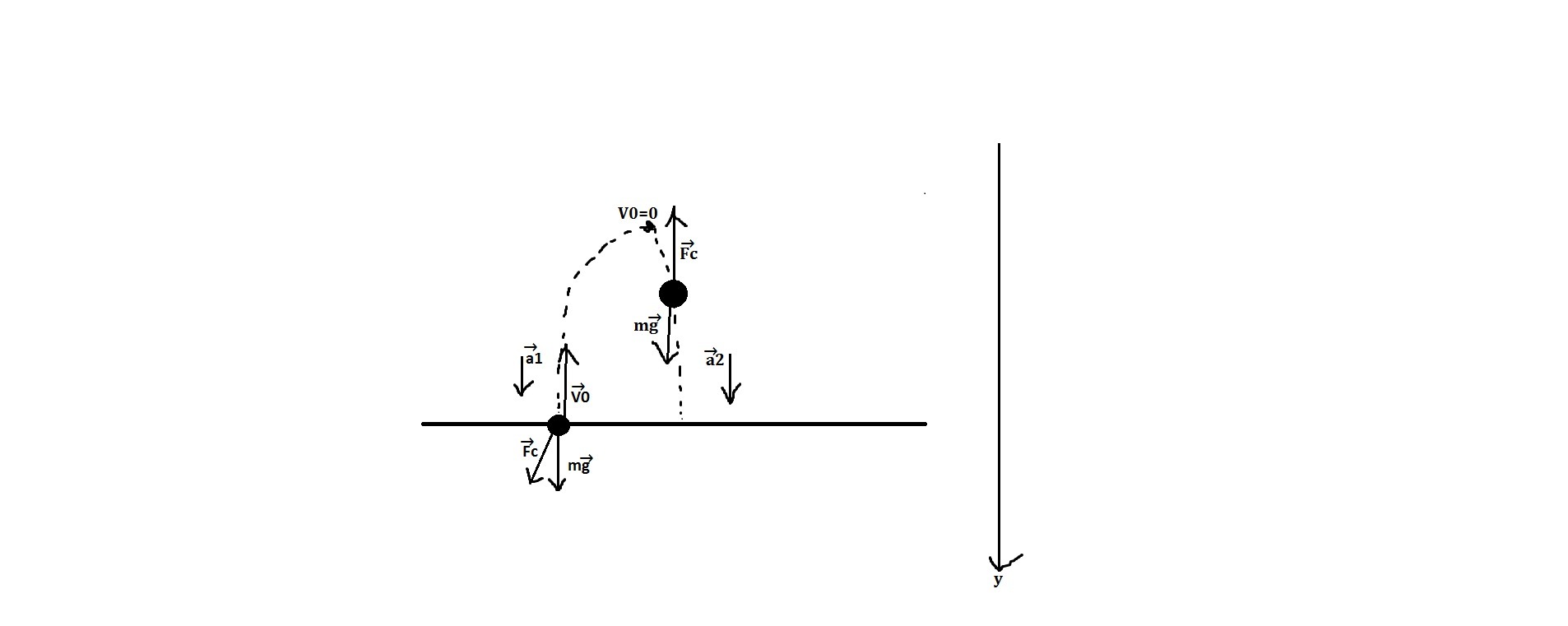
рисунок в приложении.По 2 закону Ньютона:при движении вверх:m \vec{g}+\vec{F_{c}}=m\vec{a_1}при движении вниз:m \vec{g}+\vec{F_{c}}=m\vec{a_2}проецируем на ось y:при движении вверх:mg+F_c=ma_1 \\a_1= \frac{mg+F_c}{m} при движении вниз:mg-F_c=ma_2 \\a_2= \frac{mg-F_c}{m} формула пути при движении вверх:S_n=v_0*t_n- \frac{a_1*t_{n}^2}{2} формула пути при движении вниз:v_0=0 \\S_c= \frac{a_2*t_{c}^2}{2} мы знаем, что S_c=S_nпоэтому:v_0*t_n- \frac{a_1*t_{n}^2}{2}=\frac{a_2*t_{c}^2}{2}делим все на t_{n}^2 \frac{v_0}{t_n} - \frac{a_1}{2} = \frac{a_2}{2} *( \frac{t_c}{t_n} )^2для того, чтобы найти скорость используем формулу:v^2-v_{0}^2=-2aS \\v=0 \\a=a_1 \\-v_{0}^2=-2a_1S \\v_{0}^2=2a_1S \\S_c=\frac{a_2*t_{c}^2}{2} \\v_{0}^2=2a_1*\frac{a_2*t_{c}^2}{2}=a_1*a_2*t_{c}^2 \\v_{0}=t_c*\sqrt{a_1*a_2}подставим в исходное уравнение: \frac{t_c*\sqrt{a_1*a_2}}{t_n} - \frac{a_1}{2} = \frac{a_2}{2} *( \frac{t_c}{t_n} )^2 \\ \frac{t_c}{t_n} *\sqrt{a_1*a_2}- \frac{a_1}{2} = \frac{a_2}{2} *( \frac{t_c}{t_n} )^2 \\ \frac{t_c}{t_n} =y \\y*\sqrt{a_1*a_2}-\frac{a_1}{2} = \frac{a_2}{2} *y^2 \\2y*\sqrt{a_1*a_2}-a_1=a_2*y^2 \\a_2*y^2-2y*\sqrt{a_1*a_2}+a_1=0 \\(\sqrt{a_{2}}*y)^2-2*y*\sqrt{a_{2}}*\sqrt{a_{1}}+(\sqrt{a_{1}})^2=0 \\(\sqrt{a_{2}}*y-\sqrt{a_{1}})^2=0 \\\sqrt{a_{2}}*y-\sqrt{a_{1}}=0 \\\sqrt{a_{2}}*y=\sqrt{a_{1}}y=\sqrt{ \frac{a_{1}}{a_{2}} } обратная замена:\frac{t_c}{t_n}=\sqrt{ \frac{a_{1}}{a_{2}} }\frac{t_c}{t_n}=\sqrt{ \frac{a_{1}}{a_{2}} }=\sqrt{ \frac{\frac{mg+F_c}{m}}{\frac{mg-F_c}{m}} }=\sqrt{ \frac{mg+F_c}{mg-F_c} }теперь подставляем значения:m=0,5 \\F_c=3 \\g=10 \\\frac{t_c}{t_n}=\sqrt{ \frac{0,5*10+3}{0,5*10-3} }= \sqrt{\frac{5+3}{2} }=\sqrt{4}=2Ответ: 2