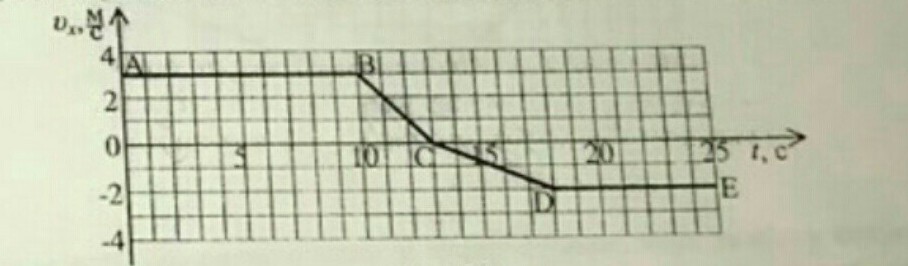
По графику зависимости проекции скорости тела от времени определить для каждого участка: а) скорость тела увеличивается или уменьшается; б) направление движения тела в) ускорение; в) путь, пройденный телом. написатм уравнения движения для каждой. участки, считая, что тело в начальный момент находилось около тела отсчета.

Пояснения к решению:Решение будет с мыслью о том, что тело движется вдоль оси X (т.е. по направлению оси или против неё).Под скоростью имеется в виду модуль вектора скорости.Под ускорением буду считать проекцию ускорения: проекция ускорения определяется как изменение проекции скорости (с учётом знака изменения) на участке делить на время этого изменения.Площадь одной клетки на графике соответсвует пути S₁ = 1 м/с * 1 с = 1 м. Путь будем определять как площадь между графиком участка и осью Х. Площадь наклонных участков (треугольники) равна площади половине произведения основания на высоту.Уравнения движения имеют вид:V₀ₓ – проекция начальной скорости на участке,aₓ – проекция ускорения на участке,В уравнениях движения не пишу размерности, значит все величины в СИ.Участок ABа) Скорость не меняется;б) Движется по направлению оси Х;в) Проекция ускорения равна 0, т.к. скорость не меняется;г) Путь = 10 клеток * 3 клетки = 30 клеток = 30 м.д) Уравнения движения:Участок BCа) Скорость уменьшается;б) Движется по направлению оси Х;в) Проекция ускорения равна (-3 м/с) / (3 с) = -1 м/с²;г) Путь = 1/2 * 3 клетки * 3 клетки = 4,5 клетки = 4,5 м.д) Уравнения движения:Участок CDа) Скорость увеличивается;б) Движется против оси Х;в) Проекция ускорения равна (-2 м/с) / (5 с) = -0,4 м/с²;г) Путь = 1/2 * 5 клеток * 2 клетки = 5 клеток = 5 м.д) Уравнения движения:Участок DEа) Скорость не меняется;б) Движется против оси Х;в) Проекция ускорения равна 0, т.к. скорость не меняется;г) Путь = 7 клеток * 2 клетки = 14 клеток = 14 м.д) Уравнения движения: