Помогите, пожалуйста, решить задачу!!!!!!

Звездная система состоит из двух звезд массами m1 и m2.
Найти период обращения звезд вокруг центра масс системы, если расстояние между центрами звезд равно L.

(Нужно выразить все по общим формулам. Сначала найти координату центра масс - х, потом период - Т.)

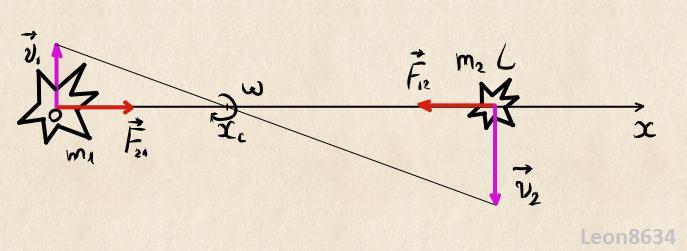
Дано:

m₁ ;

m₂ ;

L ;

__________

Найти: \displaystyle x_c, T

Решение:

Сначала найдем координату центра масс \displaystyle x_c :

\displaystyle x_c=\sum_{i}m_ix_i/\sum_{i}m_i=\frac{m_1*0+m_2L}{m_1+m_2}=\frac{m_2L}{m_1+m_2}

В соответствии с законом сохранения импульса, центр масс системы будет оставаться неподвижным, более того, он является мгновенным центром скоростей данной системы звезд, что хорошо видно из рисунка. По второму закону Ньютона, сила гравитационного притяжения между звездами сообщает первой звезде центростремительное ускорение:

\displaystyle \vec{F_{21}}=m\vec{a_c}

\displaystyle G\frac{m_1m_2}{L^2}=m_1\omega^2 x_c

\displaystyle G\frac{m_1m_2}{L^2}=m_1\omega^2\frac{m_2L}{m_1+m_2}

\displaystyle \frac{G}{L^2}=\frac{\omega^2L}{m_1+m_2}

Выразим отсюда угловую скорость вращения звезд:

\displaystyle \omega=\sqrt{\frac{G(m_1+m_2)}{L^3} }

Тогда период обращения:

\displaystyle T=\frac{2\pi }{\omega}=2\pi \sqrt{\frac{L^3}{G(m_1+m_2)} }

Ответ: \displaystyle x_c=\frac{m_2L}{m_1+m_2}  и \displaystyle T=2\pi \sqrt{\frac{L^3}{G(m_1+m_2)} } .