Помогите решить задачу модуль равнодействующей плоской системы трёх сходящихся сил

Для аналитического определения равнодействующей находятся ее проекции Rx, Ry на оси декартовой системы координат.  

Rx = ∑ Fkx ,      

Ry = ∑ Fky.

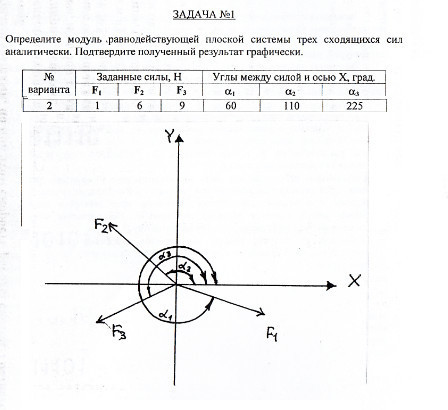
60 110 225 градусы  

1,047197551 1,919862177 3,926990817 радианы  

0,5 -0,342020143 -0,707106781 cos  

1 6 9  

0,5 -2,05212086 -6,363961031 -7,916081891 Fx

0,866025404 0,939692621 -0,707106781 sin  

0,866025404 5,638155725 -6,363961031 0,140220098 Fy

  7,917323675 F

  -0,999843156 cos α(x)

  3,123881185 радиан

  178,9852076 градус .

Графическое решение дано в приложении.

Находим углы:

β1=α1 = 60°

β2=180°-α2 = 180° - 110° = 70°

β3 = α3 - 180° = 225°-180° = 45°

Сделаем чертеж.

Проекция равнодействующей на ось ОХ:

Fx = 1*cos 60° - 6*cos 70° - 9*cos 45° = 1·0,5-6*0,342-9*0,707 ≈ - 7,9 H

Проекция равнодействующей на ось ОY:

Fy = 1*sin 60° - 6*sin 70° - 9*sin 45° = 1*0,866-6*0,940-9*0,707 ≈ - 11,1 H

По теореме Пифагора модуль равнодействующей

F ≈ √ (7,9²+11,1²) ≈ 13,7 Н

Чтобы проверить задачу графически, поступаем следующим образом:

На миллиметровой бумаге с учетом масштаба с помощью линейки и транспортира вычерчиваем векторы сил и углы. Потом по правилу сложения векторов находим равнодействующую.