-
Вблизи вертикальной стены на непроводящей и невесомой нити висит маленький шарик массой m = 3 г. Поверхность стены и шарик заряжены одноименно. Заряд шарика q = 3•10^-9 Кл. Шарик отклоняется от вертикали на угол а = 45°. Определите поверхностную плотность заряда стены. Рисунок на фото
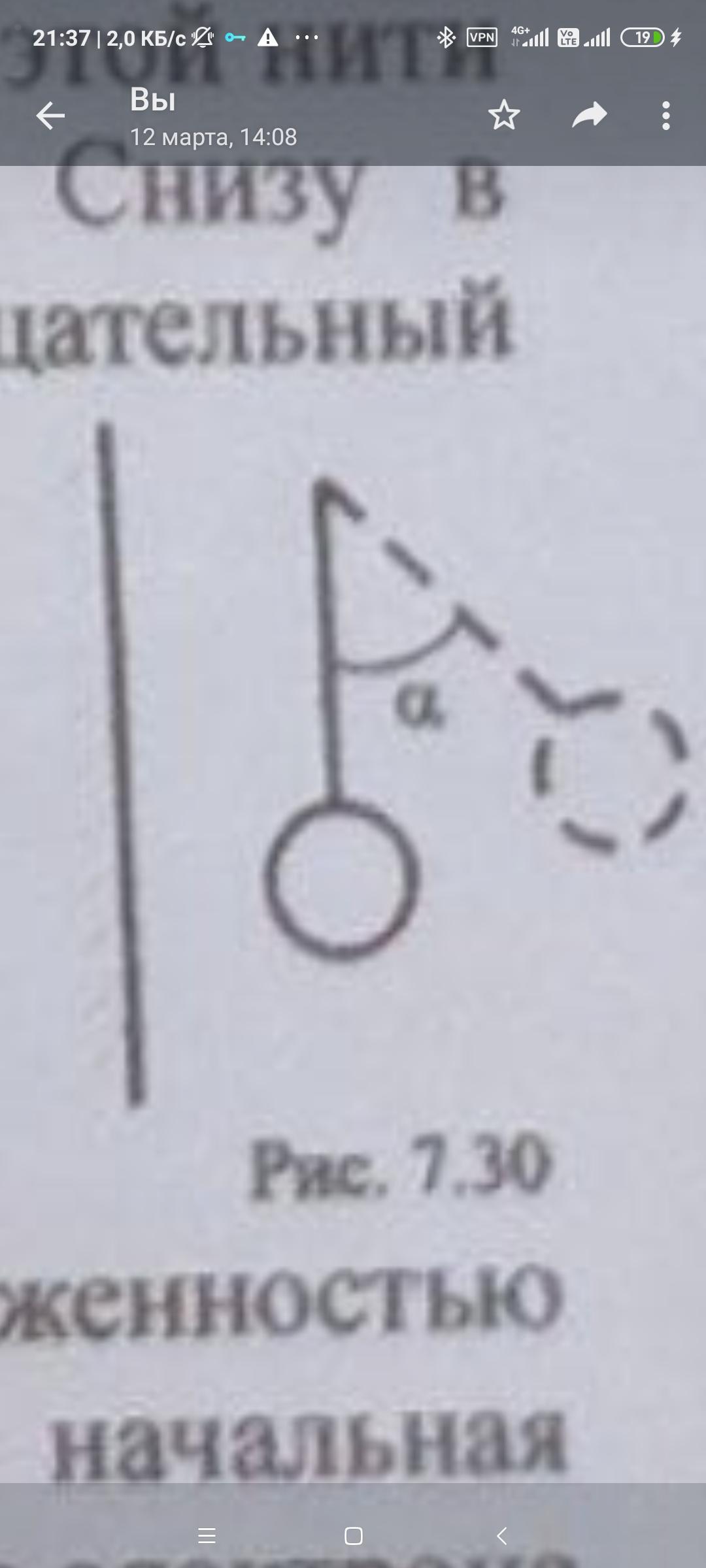
Ответы 1
-
При отклонении шарика на угол 45 градусов, сила Кулона, действующая на шарик, направлена вдоль стены и равна силе тяжести, действующей на шарик. Мы можем использовать это равенство, чтобы выразить заряд стены.
Первым шагом нам нужно вычислить силу тяжести, действующую на шарик:
F_g = m \cdot g
F
g
=m⋅g
где $m$ - масса шарика, а $g$ - ускорение свободного падения на земле ($9.8 м/с^2$). Подставляя значения, получим:
F_g = 3\cdot 10^{-3} \cdot 9.8 = 2.94 \cdot 10^{-2} H
F
g
=3⋅10
−3
⋅9.8=2.94⋅10
−2
H
Затем мы можем использовать уравнение для силы Кулона, чтобы выразить заряд стены:
F_C = \frac{1}{4\pi\epsilon_0}\frac{q^2}{r^2}
F
C
=
4πϵ
0
1
r
2
q
2
где $F_C$ - сила Кулона, действующая на шарик, $q$ - заряд шарика, $r$ - расстояние между центром шарика и стеной, а $\epsilon_0$ - электрическая постоянная ($8.85 \cdot 10^{-12} Ф/м$).
Мы можем использовать триугольник, образованный вертикальной стеной, нитью и расстоянием между центром шарика и стеной, чтобы найти расстояние $r$. Из этого треугольника следует, что:
r = \frac{l}{\sin \alpha}
r=
sinα
l
где $l$ - длина нити, а $\alpha$ - угол отклонения шарика от вертикали.
Поскольку нить невесомая, сила натяжения в нити направлена по касательной к траектории движения шарика. Таким образом, мы можем использовать уравнение для центростремительной силы, чтобы выразить нить:
F_t = \frac{m v^2}{l}
F
t
=
l
mv
2
где $v$ - скорость шарика в точке наивысшего отклонения, которую можно выразить с помощью закона сохранения энергии:
m g l \cos \alpha = \frac{1}{2} m v^2
mglcosα=
2
1
mv
2
где $mgl\cos\alpha$ - потенциальная энергия шарика в начальной точке.
Мы можем подставить это выражение для скорости в уравнение для силы натяжения, чтобы выразить длину нити:
l = \frac{m g}
-
Автор:
gizmobanq - 2 года назад
-
9
-
-
Добавить свой ответ
-
Это нормально вообще?!
-
Предмет:
Русский язык -
Автор:
aisha15 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Бесплатные баллы!!
Разбираем!!☺️☺️☺️
-
Предмет:
Математика -
Автор:
cabrera - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
11. Якими були умови життя Янко - музиканта?
-
Предмет:
Литература -
Автор:
domínguez84 - 2 года назад
-
Ответов:
1 -
Смотреть
-
- Чому США потрапили в G-7 та за яких умов
