-
Невесомый блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы а = 30° и β = 60°. Гири А и В массой 2 кг каждая соединены нитью, перекинутой через блок. Найти ускорение А, с которым движутся гири и силу натяжения нити Т. Считать нить невесомой и нерастяжимой трением пренебречь
Полное разъяснения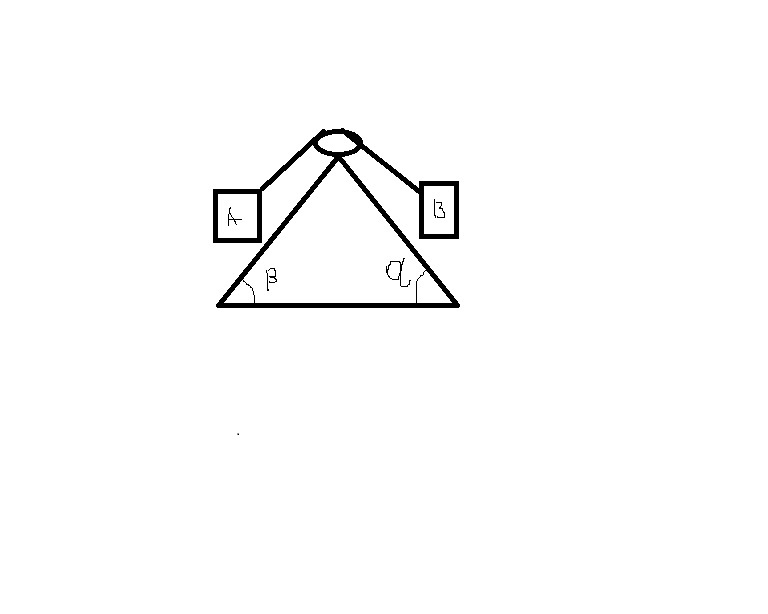
-
Предмет:
Физика -
Автор:
vanessawatson - 6 лет назад
-
Ответы 1
-
предположим, что груз В на плоскости под углом beta опускается внизтак как трения нет и массы грузов одинаковы, то задача заметно упрощаетсягруз Вma=mg*sin(beta)-Tгруз Аma=T-mg*sin(alpha)**************ma=mg*sin(beta)-Tma=T-mg*sin(alpha)*****************a=g*(sin(beta)-sin(alpha))/2 = 10*(sin(pi/3)-sin(pi/6))/2 м/с^2 = 1,830127 м/с^2T=m*g*(sin(beta)+sin(alpha))/2 = 2*10*(sin(pi/3)+sin(pi/6))/2 Н = 13,66025 Н
-
Автор:
guillermohartman - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- У скільки разів сила струму 25 кА більша за силу струму 5 кА?
-
знатные воины,жрецы-брахманы,земледельцы,слуги.что имели,чем занимались?
-
Предмет:
История -
Автор:
elishavgvq - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Периметр квадрата равен 10/13 м.Чему равна сторона квадрата?Помогите пожалуйста,умоляю.Вопрос жизни и смерти!!!-
Предмет:
Математика -
Автор:
jamarionrncc - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
какой корень в слове доставки?
-
Предмет:
Русский язык -
Автор:
barney - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
