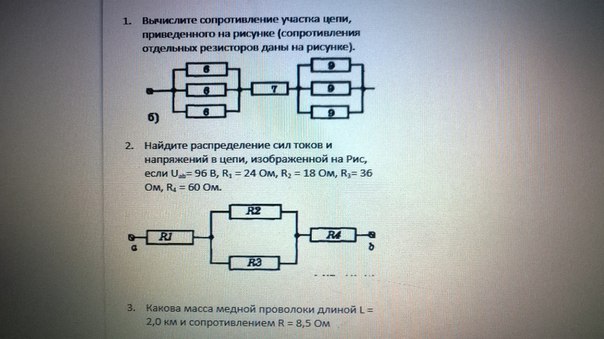
ребята,физики,помогите пожалуйста,подробно можно расписать,срочно нужно пожалуйста,20 баллов

ООО боже много,много,как я это в дз напишу все,просто надо было написать дано решение и все,просто некоторые не пишут дано,я вот и попрасила

не надо пугаться. Разберитесь с решением, и сами сообразите, как оформить "Дано" и "Решение"

хорошо,спасибо большое)

1. Данную цепь сопротивлений можно представить в виде рис1. R1 - эквивалентно трем первым сопротивлениям, соединенным параллельно. R2 - эквивалентно трем другим сопротивлениям, так же соединенным параллельно. При параллельном соединении "n" сопротивлений их суммарное сопротивление  определяется выражением 1/Rсуммарное = 1/R1 + 1/R2 + 1|R3 +... + 1/Rn. В нашем случае имеем 1/R1 = 1/6 + 1/6 + 1/6 =3/6 = 1/2. Отсюда R1 = 2 Ома.  Аналогично для R2.   1/R2 = 1/9 + 1/9 + 1/9 = 3/9 = 1/3.  Отсюда R2 = 3 Ома. Дальше видим, что   R1, R = 7 Ом  и  R2 соединены последовательно. При таком соединении суммарное сопротивление равно сумме всех соединенных последовательно сопротивлений. Т.е. = R1 + R + R2. Таким образом полное сопротивление всей цепи равно 2 + 7 + 3 = 12 Ом 2. Чтобы найти токи, текущие в цепи, надо найти сопротивление всей цепи. Найдем вначале сопротивление среднего участка цепи с сопротивлениями R2 и R3. По аналогии с первой задачей можно записать, что 1/R(2-3) =  1/R2 + 1/R3. Отсюда R(2-3) = R2*R3/(R2+R3) = 18*36/(18+36) = 12 Ом. Полное сопротивление участка a-b  - Rab =  R1 + R(2-3) + R4 = 24 + 12 + 60 = 96 Ом. По закону Ома ток, текущий в цепи I = U/R, здесь U - напряжение на концах цепи;  R- сопротивление цепи. Таким образом ток в цепи Iab = Uab/Rab = 96/96 = 1 A. Такой ток будет течь через сопротивления 1 и 4. Но этот ток будет сначала разделяться в одном узле. И через сопротивления 2 и 3 будут течь токи, сумма которых будет равняться 1А. а затем, в другом узле эти токи суммируются и их сумма опять станет равной 1А. Следовательно можно записать, что I2 + I3 = 1 A. При параллельном соединении сопротивлений токи в них разделяются пропорционально величинам сопротивлений. Т.е. во сколько раз одно сопротивление больше другого, то ровно во столько же раз ток в этом сопротивлении будет меньше тока в другом сопротивлении. Значит можно записать соотношение I2/I3 = R3/R2. Таким образом, имеем систему уравнений: I2 + I3 = 1 A I2/I3 = R3/R2. Решая систему уравнений, например, выразив из первого уравнения  I2 = 1 - I3,  запишем второе уравнение в виде (1-I3)/I3 = R3/R2.  Отсюда I3 = R2/(R2+R3) = 18/56 =1/3 А. Тогда I2 = 1 - 1/3 = 2/3 А. Падение напряжения на участке цепи равно произведению тока на этом участке на сопротивление участка. Т.е. падение напряжения на участке, например, a-b Uab = Iab*Rab = 1 * 96 = 96 Вольт.  Это падение напряжения должно равняться сумме падений напряжений на всех участках цепи. Падение напряжение на участке с R1 будет U1 = Iab*R1 = 1*24 = 24 В.   U2-3 = Iab*R(2-3)  = 1 * 12 = 12 B. U4 = Iab*R4 = 1*60 = 60 B. Как видим сумма падений напряжений на трех участках цепи равна падению напряжения на участке a-b, как и должно быть.  U2 = I2*R2 = (2/3)*18= 12 В. U3 = I3*R3 = (1/3)*36 = 12 В. Как видим, падение на сопротивлении 2 равно падению напряжения на сопротивлении 3. Точно так и должно быть, т.к. проводники, слева от сопротивлений, приходят в один узел, а справа от сопротивлений в другой.  А разность потенциалов (падение напряжения) между обними и теми же узлами не может быть различной для различных сопротивлений соединенных с этими узлами. 3. Надо найти площадь сечения (S) проволоки. Известно, что сопротивление проволоки определяется выражением R = p*L/S. Здесь р - удельная проводимость меди = 0,017 Ом*мм^2/м:  S - площадь сечения проволоки.  Найдя S и умножив на длину проволоки найдем её объем, а зная объем и плотность меди найдем массу проволоки. Из уравнения для сопротивления проволоки можно найти S= p*L/R = 0,017*2000/8,5 = 34/8,5 = 4 мм^2= 4*10^-6 м^3 Объем этой проволоки V = S*L= 4*10^-6 *2000 = 0,008 м^3. Плотность меди P= 8920 кг/м^3.  И масса проволоки m = P*V = 8920 * 0,008 = 71,36 кг.