Указать подобные треугольники доказать их подобие

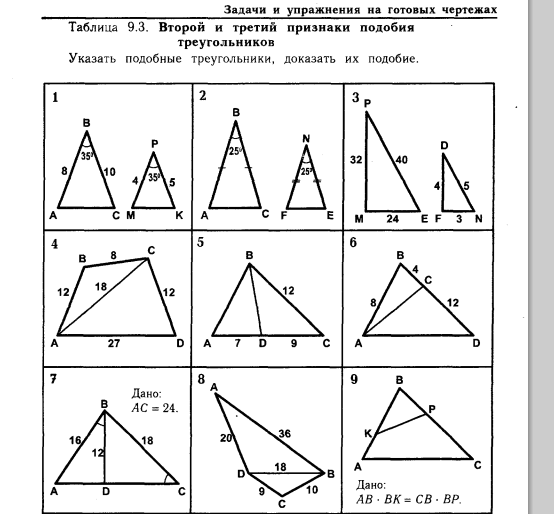
1. АВ : МР = ВС : РК = 2 : 1,

∠В = ∠Р, ⇒ ΔАВС подобен ΔМРК по двум пропорциональным сторонам и углу между ними.

2. ΔАВС равнобедренный, значит ∠А = ∠С = (180° - 25°)/2 = 77,5°.

ΔFNE равнобедренный, значит ∠F = ∠E = (180° - 25°)/2 = 77,5°.

Итак, ∠В = ∠N, ∠A = ∠F, ⇒ ΔАВС подобен ΔFNE по двум углам.

3. PM : DF = 32 : 4 = 8 : 1

PE : DN = 40 : 5 = 8 : 1

ME : FN = 24 : 3 = 8 : 1

значит ΔPME подобен ΔDFN по трем пропорциональным сторонам.

4. BC : CD = 8 : 12 = 2 : 3

AB : AC = 12 : 18 = 2 : 3

AC : AD = 18 : 27 = 2 : 3,

значит ΔАСВ подобен ΔADC по трем пропорциональным сторонам.

5. CD : CB = 9 : 12 = 3 : 4

CB : AC = 12 : 16 = 3 : 4, угол С общий для треугольников BCD и АСВ, значит эти треугольники подобны по двум пропорциональным сторонам и углу между ними.

6. ВС : АВ = 4 : 8 = 1 : 2

АВ : BD = 8 : 16 = 1 : 2

угол В общий для треугольников АВС и DBA, значит эти треугольники подобны по двум пропорциональным сторонам и углу между ними.

7. BD : BC = 12 : 18 = 2 : 3

AB : AC = 16 : 24 = 2 : 3,

∠ABD = ∠ACB по условию, ⇒ ΔABD подобен  ΔACB по двум пропорциональным сторонам и углу между ними.

8. DC : DB = 9 : 18 = 1 : 2

BC : AD = 10 : 20 = 1 : 2

BD + AB = 18 : 36 = 1 : 2, ⇒

ΔBDC подобен ΔABD по трем пропорциональным сторонам.

9. АВ · ВК = СВ · ВР

Разделим обе части данного равенства на (СВ ·АВ), получим:

ВК : СВ = ВР : АВ, угол В общий для треугольников КВР и СВА, значит они подобны по двум пропорциональным сторонам и углу между ними.