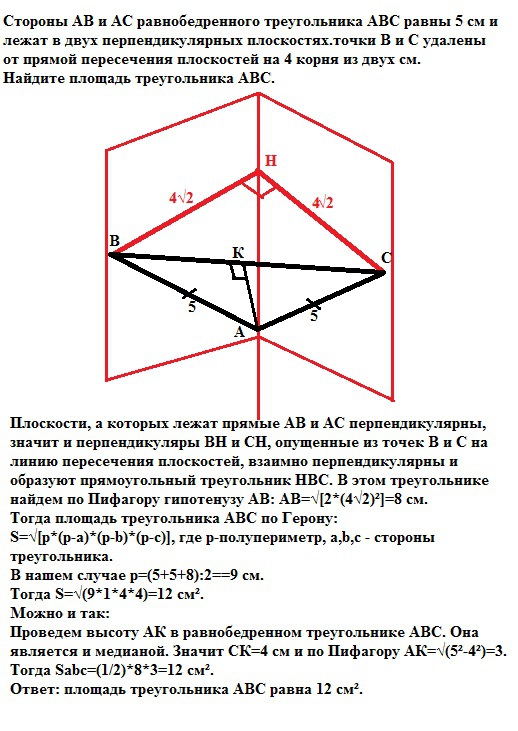
стороны АВ и АС равнобедренного треугольника АВС равны 5 см и лежат в двух перпендикулярных плоскостях.точки В и С удалены от прямой пересечения плоскостей на 4 корня из двух см. найдите площадь треугольника

Плоскости, а которых лежат прямые АВ и АС перпендикулярны, значит и перпендикуляры ВН и СН, опущенные из точек В и С на линию пересечения плоскостей, взаимно перпендикулярны и образуют прямоугольный треугольник НВС. В этом треугольнике найдем по Пифагору гипотенузу ВС: ВС=√[2*(4√2)²]=8 см.Тогда площадь треугольника АВС по Герону:S=√[p*(p-a)*(p-b)*(p-c)], где р-полупериметр, a,b,c - стороны треугольника.В нашем случае р=(5+5+8):2==9 см.Тогда S=√(9*1*4*4)=12 cм².Можно и так:Проведем высоту АК в равнобедренном треугольнике АВС. Она является и медианой. Значит СК=4 см и по Пифагору АК=√(5²-4²)=3. Тогда Sabc=(1/2)*8*3=12 cм².Ответ: площадь треугольника АВС равна 12 см².