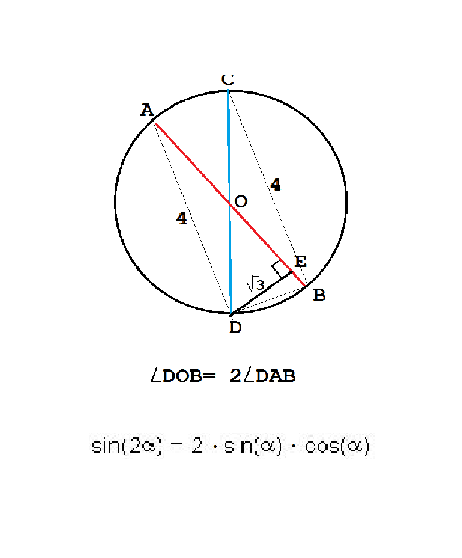
В окружности AB и CD - два не взаимно перпендикулярных диаметра, DE перпендикулярно AB, СВ=4, DE=Корень из трех. Найдите острый угол между диаметрами.
Объясните, как решать, не понимаю.
И желательно с рисунком.

Пусть центр окружности будет О, и это точка пересечения диаметров. Треугольники АOD и  COE  равны - их  углы равны: при О - как вертикальные, а острые углы вписанные и опираются на равные дуги, ко всему эти треугольники еще и равнобедренные, и на основании  этого тоже углы равны. Треугольник АЕD - прямоугольный по условию. DE - катет, AD - гипотенуза. Из доказанного выше равенства треугольников АD=CB=4, тогда синус А= DE:AD=(√3):4Острый угол DOВ между диаметрами - центральный угол, который опирается на ту же дугу, что угол DАЕ  Следовательно,∠DOВ равен 2* ∠DABsin∠DAE=DE:AD=(√3):4Синус DOB найдем по формуле = sin 2α=2*sin(α)*cos(α)Косинус α =АЕ:ADАЕ из прямоугольного треугольника  AED по т.Пифагора АЕ=√(16-3)=√13cos∠DAE=(√13):4Тогда sin DOB=[2*(√3):4]*[(√13):4])= (√39):8=0,7806 и ∠ DOB=arcsin 0,7806--------------------------- Или:Треугольник АDB - прямоугольный ( ADB опирается на диаметр АВ). DE в нем высота, квадрат которой равен произведению DE²=АЕ*ВЕ3=(√13)*ВЕВЕ=3:√13Тогда диаметр  равен АЕ+ВЕ=√13+3:√13=16:√13, а радиус ОВ=ОD=8:√13Тогда синус DOB=DE:OD=(√3):(8:√13)= (√39):8=0,7806и угол DOB=arcsin 0,7806 По таблице синусов можно найти его градусную величину: 51°20'---------------И "на закуску" то, с чего можно было начать и остановиться на этом. Ясно,  что найдя синус угла DAE, мы можем по таблице найти этот угол, а умножив на два  его значение, найти искомый угол DOE. Итак, синус ∠DAE=(√3):4=0,4330. По таблице синусов это синус угла 25° 40'. ⇒∠ DOВ=2*25° 40'=51°20'------bzs@