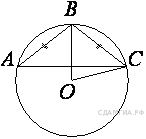
Окруж­ность с цен­тром в точке O опи­са­на около рав­но­бед­рен­но­го тре­уголь­ни­ка ABC, в ко­то­ром AB = BC и ∠ABC = 177°. Най­ди­те ве­ли­чи­ну угла BOC. Ответ дайте в гра­ду­сах.

спасибо огромное :3

Центр описанной окружности располагается на пересечении серединных перпендикуляровтреугольника. Так как треугольник равнобедренный, то биссектриса и серединный перпендикуляр, проведенные к основанию, совпадают.Следовательно, BO - биссектриса угла ABC.Тогда: ∠CBO=∠ABC/2=177°/2=88,5°Треугольник OBC - равнобедренный, так как OB и OC - радиусы окружности и следовательно равны.По свойству равнобедренного треугольника:∠CBO=∠BCO=88,5°По теореме о сумме углов треугольника:180°=∠CBO+∠BCO+∠BOC180°=88,5°+88,5°+∠BOC∠BOC=3°Ответ: 3