помогите пожалуйста решить, (желательно с рисунком), спасибо

помогите пожалуйста решить, (желательно с рисунком), спасибо
- Предмет:
  Геометрия
- Автор:
  tucker28
- 6 лет назад

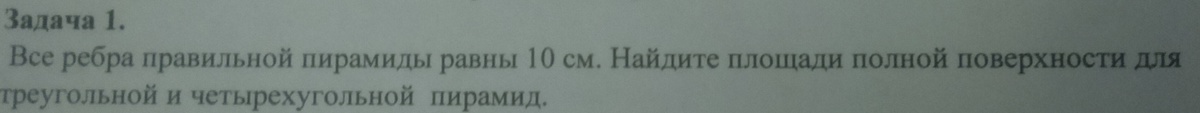
Ответы 2

Спасибо!!!
- Автор:
  red6of2
- 6 лет назад
- 0
S(пол) = Sосн + SбокРисунок 1.Правильная четырёхугольная пирамида, в основе лежит квадратSосн = $AD^2=100$ см²Забыл провести апофему (SK - высота треугольника SCD есть и апофема пирамиды)По радиусу вписанной окружности $r=OK= \frac{AD}{2} =5$ смOD - радиус описанной окружности $OD= \dfrac{ \frac{AD}{2} }{\sin \frac{180}{n} } = \frac{5}{\sin45а}=5 \sqrt{2}$ смС треугольника SOD(<SOD = 90градусов) $SO= \sqrt{SD^2-OD^2} = \sqrt{100-50} =5 \sqrt{2}$ С треугольника SOK(<SOK = 90 градусов) $SK= \sqrt{OK^2+SO^2} = \sqrt{50+25} =5 \sqrt{3}$ смПлощадь боковой поверхности: $S_{bok}= \frac{1}{2} \cdot P_{ocH}\cdot SK= \frac{1}{2}\cdot 4\cdot 10\cdot 5 \sqrt{3} =100 \sqrt{3}$ см²Найдем площадь полной поверхности $S=100+100 \sqrt{3}=100(1+\sqrt{3})$ см²Ответ: $100(1+\sqrt{3})$ СМ²Рисунок 2.Правильная треугольная пирамида(в основе лежит правильный треугольник) $S_{ocH}= \frac{AB^2 \sqrt{3} }{4} = \frac{100\sqrt{3} }{4} =25\sqrt{3}$ см²SK - высота треугольника SCB(также является апофемой пирамиды)CK=KB=BC/2=5 смС прямоугольного треугольника SKB(<SKB=90градусов) $SK= \sqrt{100-25} =5 \sqrt{3}$ смНаходим площадь треугольника SCB $S_{SCB}= \frac{BC\cdot SK}{2} =25 \sqrt{3}$ см²Так как у пирамиды три грани то площадь боковой будет $S_{bok}=3\cdot S_{SCB}=75\sqrt{3}$ см²И так площадь полной поверхности $S=S_{o}+S_{bok}=25\sqrt{3} +75\sqrt{3} =100\sqrt{3}$ см²Ответ: $100\sqrt{3}$ см²
- Автор:
  bretthbov
- 6 лет назад
- 0
Добавить свой ответ