На рисунке 50 треугольник ABC - равнобедренный

№1

1.1. 

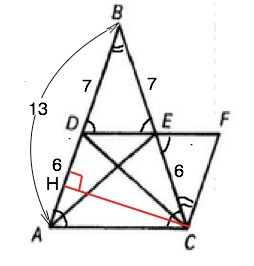
Докажите, что ∆ АDЕ=∆ СЕD. 

В четырехугольнике АDFС противоположные стороны попарно параллельны ( дано) 

Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм

∆ АВС- равнобедренный, DЕ||АС=> 

Углы ∆ DBE при основании DE  равны углам ∆ АВС при основании АС.

∆ BDC~∆ ABC по равным углам. => 

∆  BDE- равнобедренный. ВD=BE=7.

AB=BC=13

AD=EC=13-7=6

<BDE=<BED.

<АDE=<CED - смежные им

В ∆ АDЕ и ∆ СЕD  равны две стороны и угол между ними. 

∆ АDЕ=∆ СЕD по 1-му признаку равенства треугольников.  

1.2.

Докажите, что ∆ ЕСF~∆ АВС

СF||АВ, ВС - секущая, => накрестлежащие ∠АВС=∠ВСF . 

Углы при Е равны как вертикальные. ∆ ЕСF~∆ АВС по двум равным углам. 

1.3

Найдите ЕF. 

Из доказанного выше подобия ∆ ЕСF и ∆ АВС следует отношение:

ЕF:АС=ЕС:СВ; ЕF:10=6:13=> ЕF=60/13

1.4.

Найдите высоту ∆ АВС, опущенную на боковую сторону. 

По ф. Герона: 

S=√[p•(p-a)•(p-b)•(p-c)], где р - полупериметр, а, b и с - стороны.

p=(13+13+10):2=18

S=√[18•5•5•8]=√[9•2•5•5•4•2]=3•4•5=60

Из другой формулы площади треугольника 

S=a•h:2 найдем высоту h опущенную на АВ. 

S=60=>   h=2S:АВ=120:13=9 ³/₁₃

1.5

Найдите отношение S(ADE):S(DCF)

Т.к. АDFС параллелограмм, DF=АC=10 

DE║AC, поэтому высоты ∆ ADE и ∆ DCF равны. 

Отношению площадей треугольников с равными высотами равно отношению их оснований. 

S(ADE):S(DCF)=DE:DF

DE=DF-EF=10-(60/13)=70/13

DE:DF=(70/13):10=7/13

S(ADE):S(DCF)=7/13

–––––––––––––––––––––––––

2.

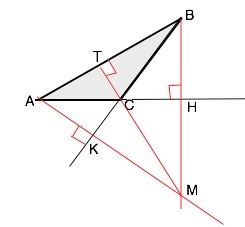
Высоты треугольника пересекаются в одной точке. 

Высоты, проведенные из вершин острых углов тупоугольного треугольника, расположены вне треугольника и пересекают продолжения сторон, к которым проведены. 

На рисунке ∆ АВС - тупоугольный. АК, ВН и СТ - его высоты.  

М - искомая точка.