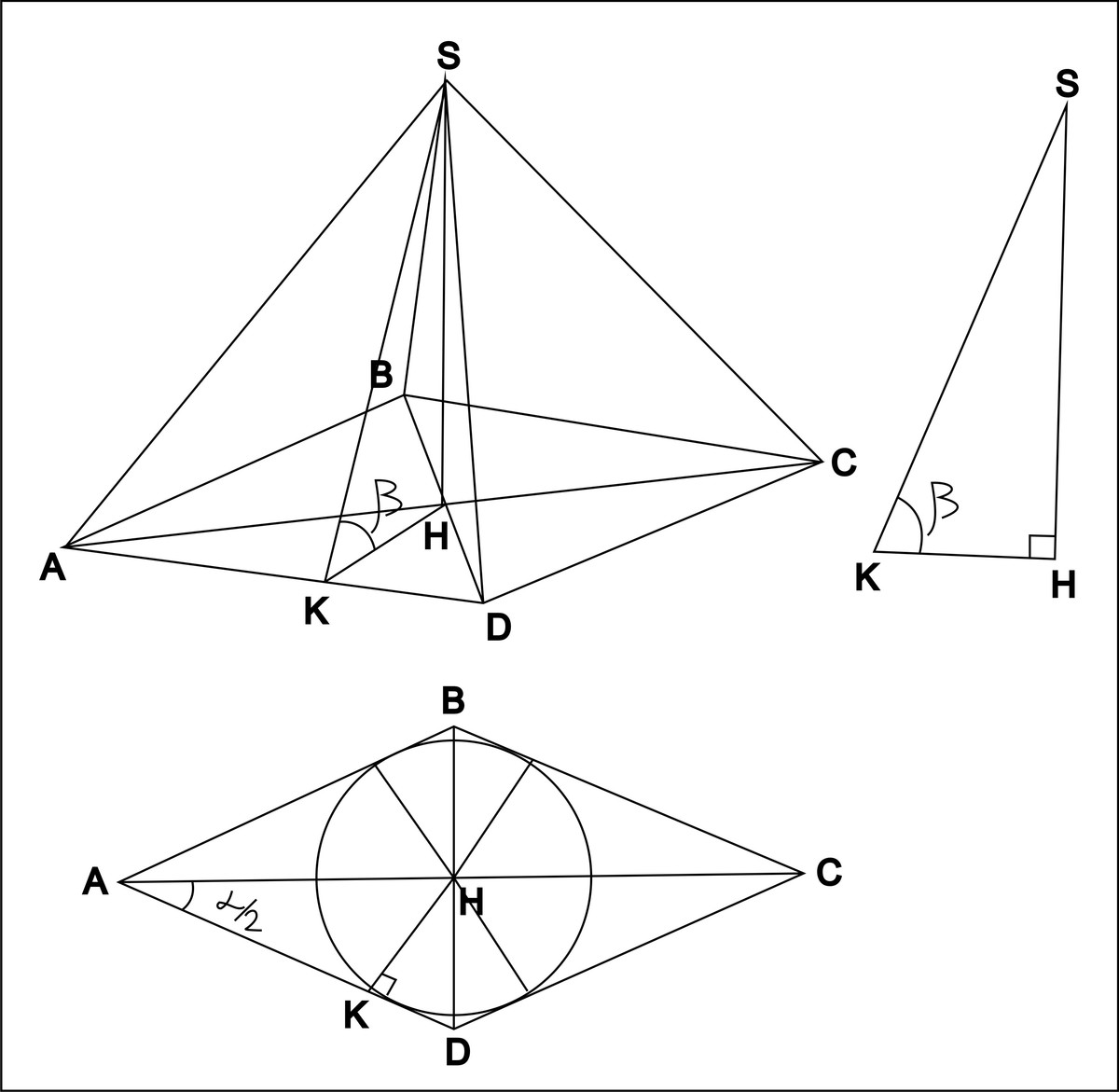
основание пирамиды ромб с острым углом альфа. высота пирамиды Н,а все двугранные углы при основании бета . докажите,что высота проходит через точку пересечения диагоналей и найдите площадь полной поверхности

а)если высота пирамиды H, то КН=Н/tgбеттаэто действенно для каждой боковой грани пирамиды, высота везде одинаковая и двугранный угол тожето есть точка Н равноудалена от сторон основаниято есть точка Н является центром вписанной в ромб окружностицентр вписанной в ромб окружности лежит на биссетрисах углов, то есть на пересечении диагоналей ромбаб)величины получаются с помощью тригонометрических функций прямоугольного треугольникаsin(альфа/2)=КН/АНКН=Н/tgбеттаАН=Н/(tgбетта*sin(альфа/2))tg(альфа/2)=HD/AHHD=H/(tgбетта*cos(альфа/2))S(основания)=2*(Н/(tgбетта*sin(альфа/2)))*(H/(tgбетта*cos(альфа/2)))=(4H^2)/(tg^2(бетта)sinальфа)AD=H/(tgбетта*sin(альфа/2)*cos(альфа/2))=2Н/(tgбетта*sinальфа)Площадь каждой боковой грани равна S (боковой поверхности)=4*(1/2)*(Н/sinбетта)*(2Н/(tgбетта*sinальфа))=(4Н^2)/(tgбетта*sinальфа*sinбетта)S(общая)=(4Н^2(sinбетта+tgбетта))/(tg^2(бетта)*sinальфа*sinбетта)